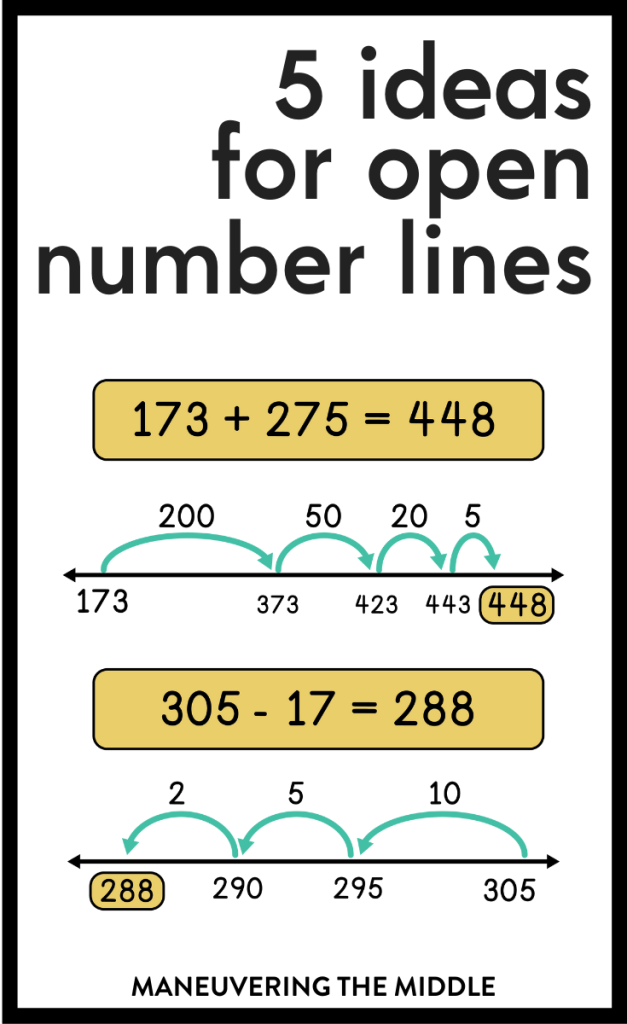
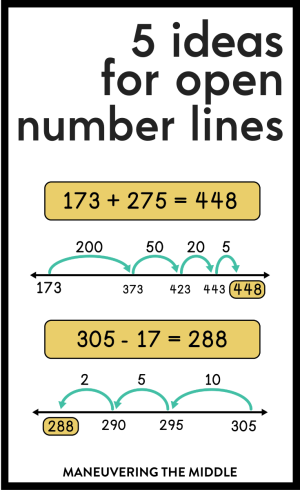
What is an Open Number Line? An open number line is exactly what it sounds like – a blank number line that students can use to solve a multitude of middle school math problems. Open number lines provide a great visual for abstract concepts.
Let’s talk about 5 ways to use open number lines in middle school math!
1. Fluency
Adding friendly numbers – This method leaves one addend whole and adds the other addend in friendly amounts.
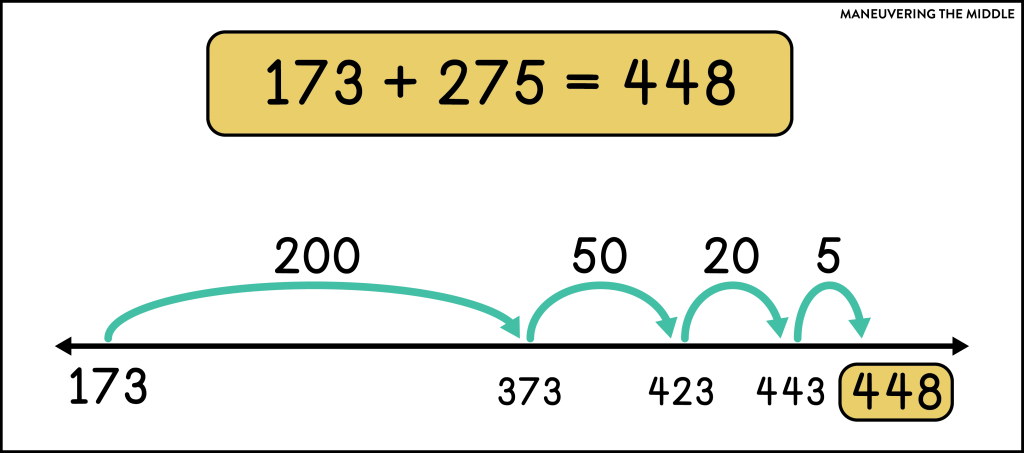
In this example, 275 was added to 173 in friendly chunks of 200, 50, 20, and 5 to get the final sum of 448.
Adding to friendly numbers – This method adds a small amount first to get a partial sum that is friendly, then adds the remaining amount in friendly chunks.
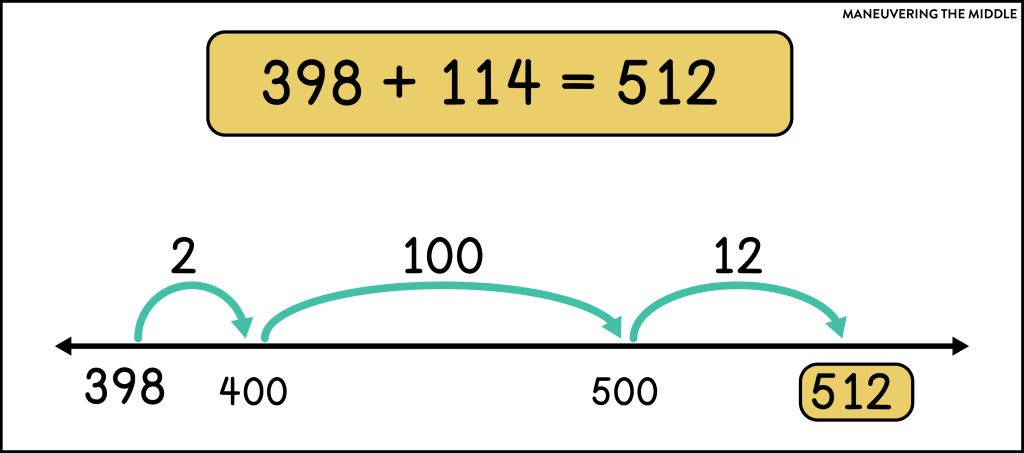
In this example, 2 was added to 398 to get the friendly number of 400. Then, the remaining 112 was added in chunks of 100 and 12 to get the final sum of 512.
Distance (Subtraction) – Because subtraction is the distance between the two values, students can use an open number line to count up to the total distance between the two numbers. Values closer together are better suited for this method.
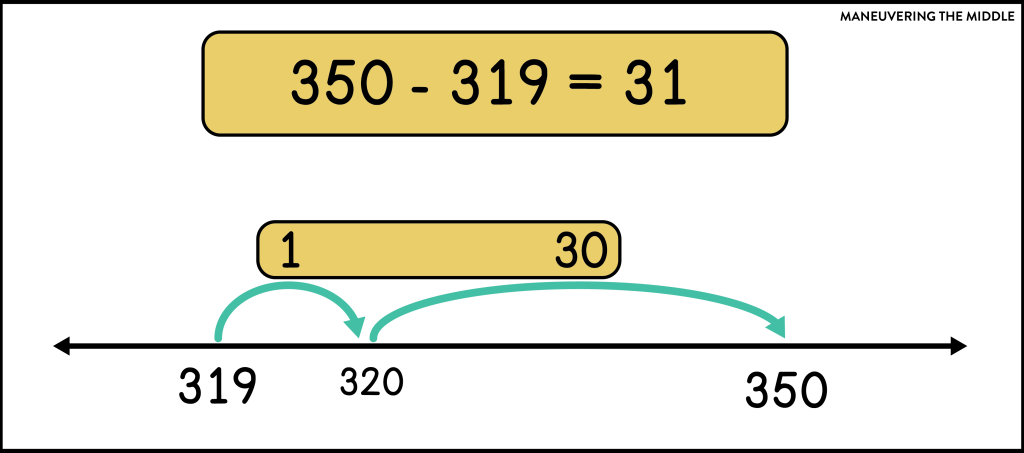
Removal (Subtraction) – Removal takes away to find the difference between two values. Values further apart may be easier to subtract using removal.
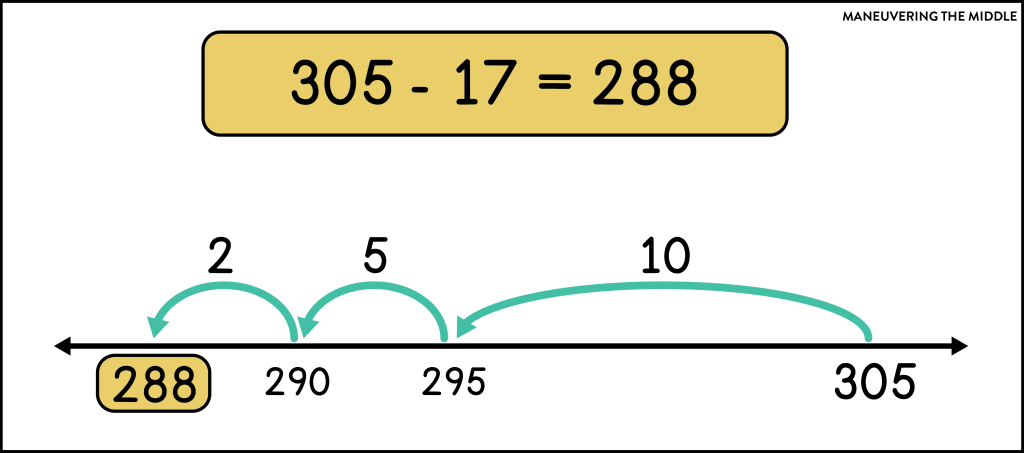
Constant Difference – Add or subtract the same number from both values to make the numbers easier while keeping a constant difference.
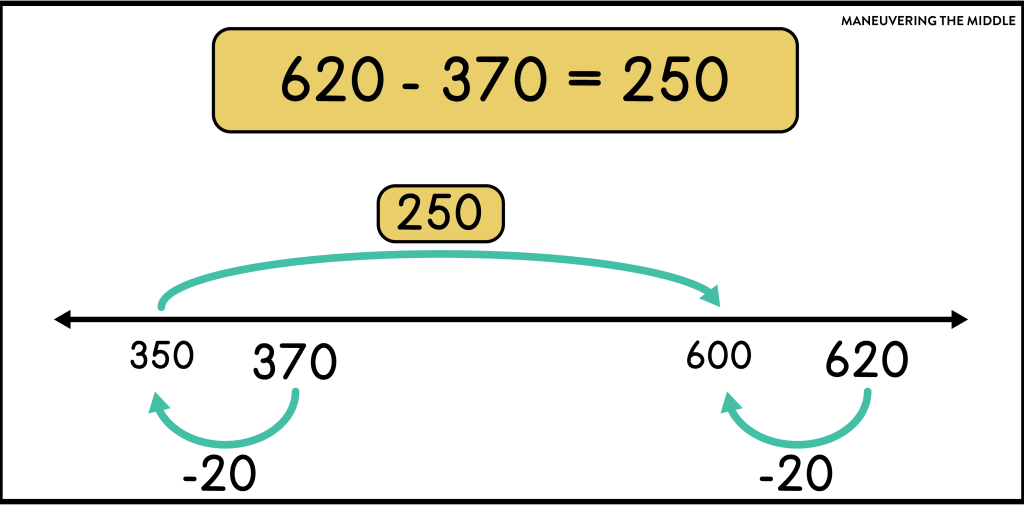
In this example, 620-370 was adjusted by subtracting 20 from each value (620-20=600 and 370-20=350) and finding the difference between 600-350. (I could have added 30 to 370 and 620 too!)
2. Ratios and Conversions
Double Number Lines – Double number lines are useful for ratios and conversions. If you typically use a table for solving ratio problems, then an open number line is not too far off.

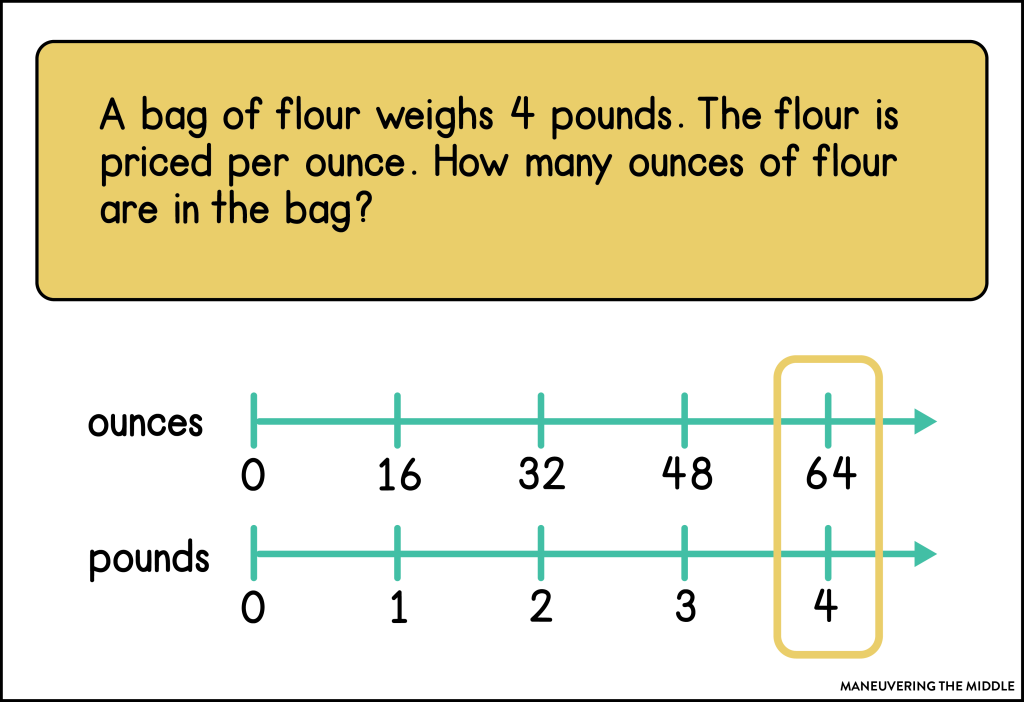
3. Ordering Numbers
You can read more about this in our Ordering Rational Numbers post, but ultimately, no problem that involves ordering numbers is complete without a number line. It provides context and is a way to actually show student thinking.
While starting with a completely blank number line can work for some students, I recommend writing in whole numbers first.
Example: -½, -2.2, -1.5
Before placing a single number from above on an open number line, I would ask students to provide the integer numbers (for simplicity sake, I am referring to -3, -2, -1, and 0) that make sense with the numbers provided in the example.
Once determined, students will have a much easier job placing -1.5 between -2 and -1 than on a blank number line with -½ and -2.2.
Hint: Use a vertical number line when involving negative numbers.
4. Problem Solving
These problem solving strategies are best explained in word problem format. Please read the word problems to fully understand the open number line diagrams.
Active Situations – This method describes a situation in which quantities are joined or removed. There is a start, a change, and a result.

Part Part Whole – This describes a relationship that includes two or more parts that relate to a whole.
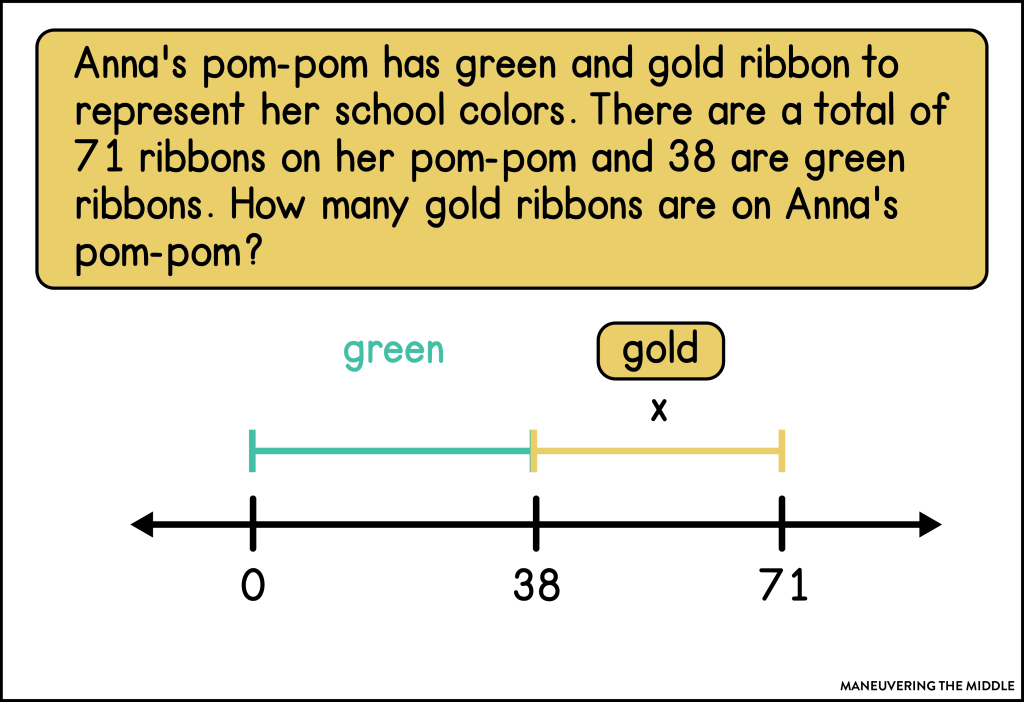
Additive Comparisons – These are situations that describe how two quantities compare to each other. They include a smaller quantity, a larger quantity, and the difference between the two quantities.
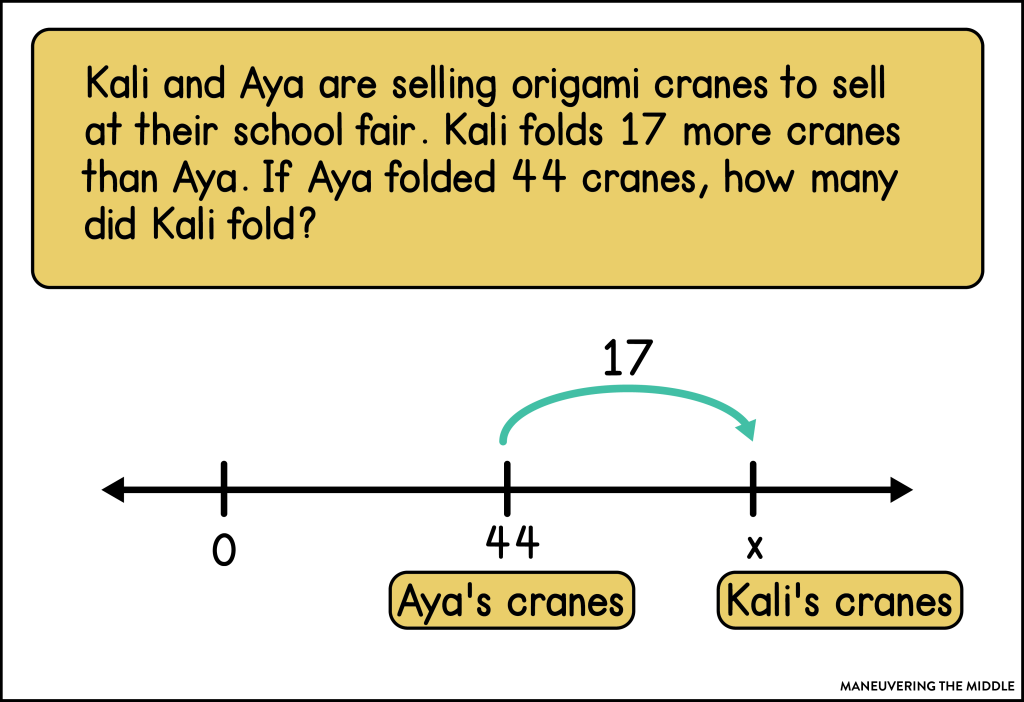
I had no idea there are so many ways to use number lines to solve so many different types of middle school math problems. Do you use open number lines?
If you are interested in learning more about open number lines, our Maneuvering Math Intervention Program will be adding a new module called Jump Start in time for Back to School Season! Jump Start is an introductory component to equip students with tools and strategies for number operations and problem solving.
It will help students reason with numbers, recognize and effectively represent problem-solving situations and approach math with increased confidence and tools to use throughout challenging concepts.