How many times have you been teaching a concept that students are feeling confident in, only for them to completely shut down when faced with a word problem? For me, the answer is too many to count. Word problems require problem solving strategies. And more than anything, word problems require decoding, eliminating extra information, and opportunities for students to solve for something that the question is not asking for. There are so many places for students to make errors! Let’s talk about some problem solving strategies that can help guide and encourage students!

Math Problem Solving Strategies
1. C.U.B.E.S.
C.U.B.E.S stands for circle the important numbers, underline the question, box the words that are keywords, eliminate extra information, and solve by showing work.
- Why I like it: Gives students a very specific ‘what to do.’
- Why I don’t like it: With all of the annotating of the problem, I’m not sure that students are actually reading the problem. None of the steps emphasize reading the problem but maybe that is a given.

2. R.U.N.S.
R.U.N.S. stands for read the problem, underline the question, name the problem type, and write a strategy sentence.
- Why I like it: Students are forced to think about what type of problem it is (factoring, division, etc) and then come up with a plan to solve it using a strategy sentence. This is a great strategy to teach when you are tackling various types of problems.
- Why I don’t like it: Though I love the opportunity for students to write in math, writing a strategy statement for every problem can eat up a lot of time.
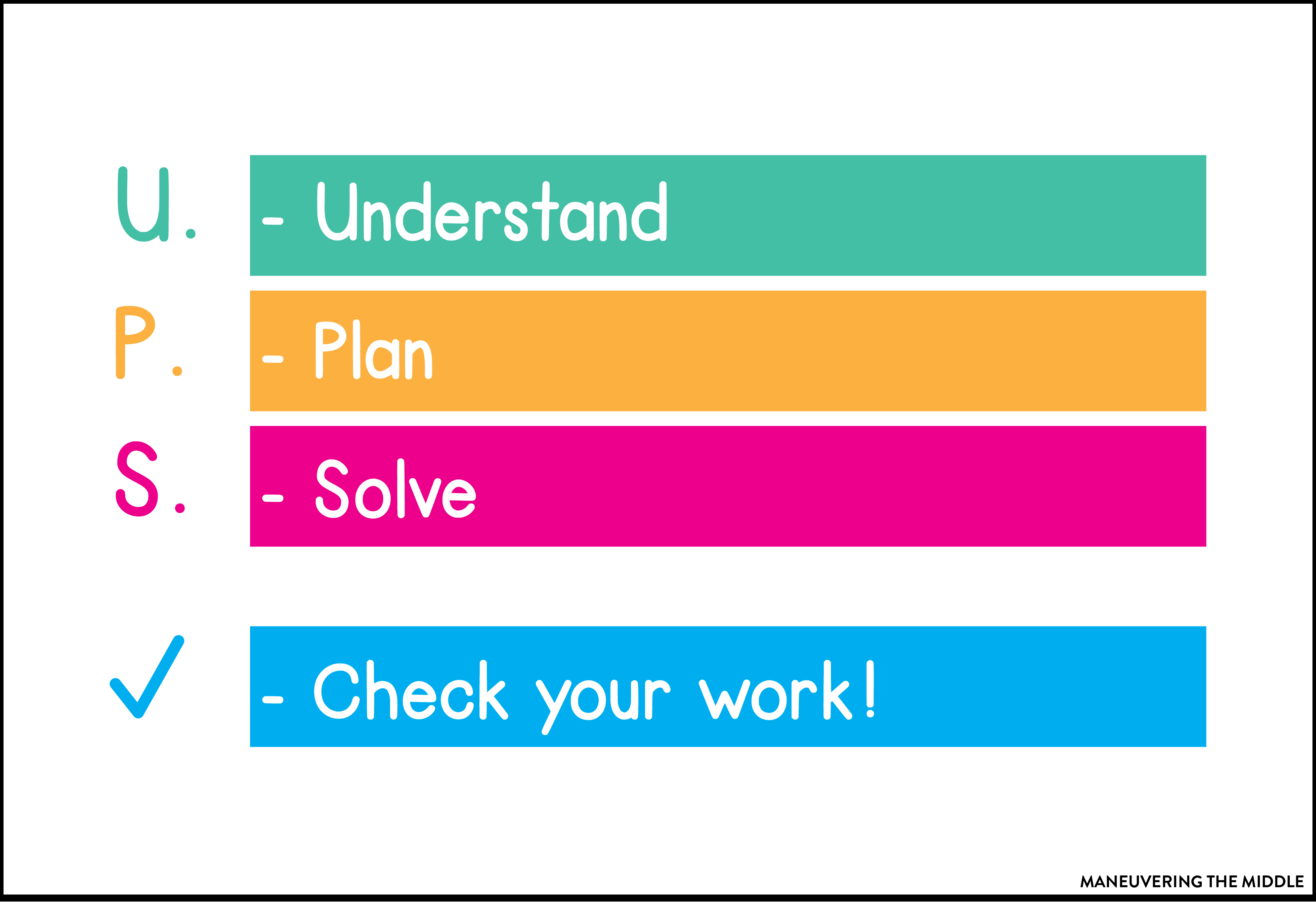
3. U.P.S. CHECK
U.P.S. Check stands for understand, plan, solve, and check.
- Why I like it: I love that there is a check step in this problem solving strategy. Students having to defend the reasonableness of their answer is essential for students’ number sense.
- Why I don’t like it: It can be a little vague and doesn’t give concrete ‘what to dos.’ Checking that students completed the ‘understand’ step can be hard to see.
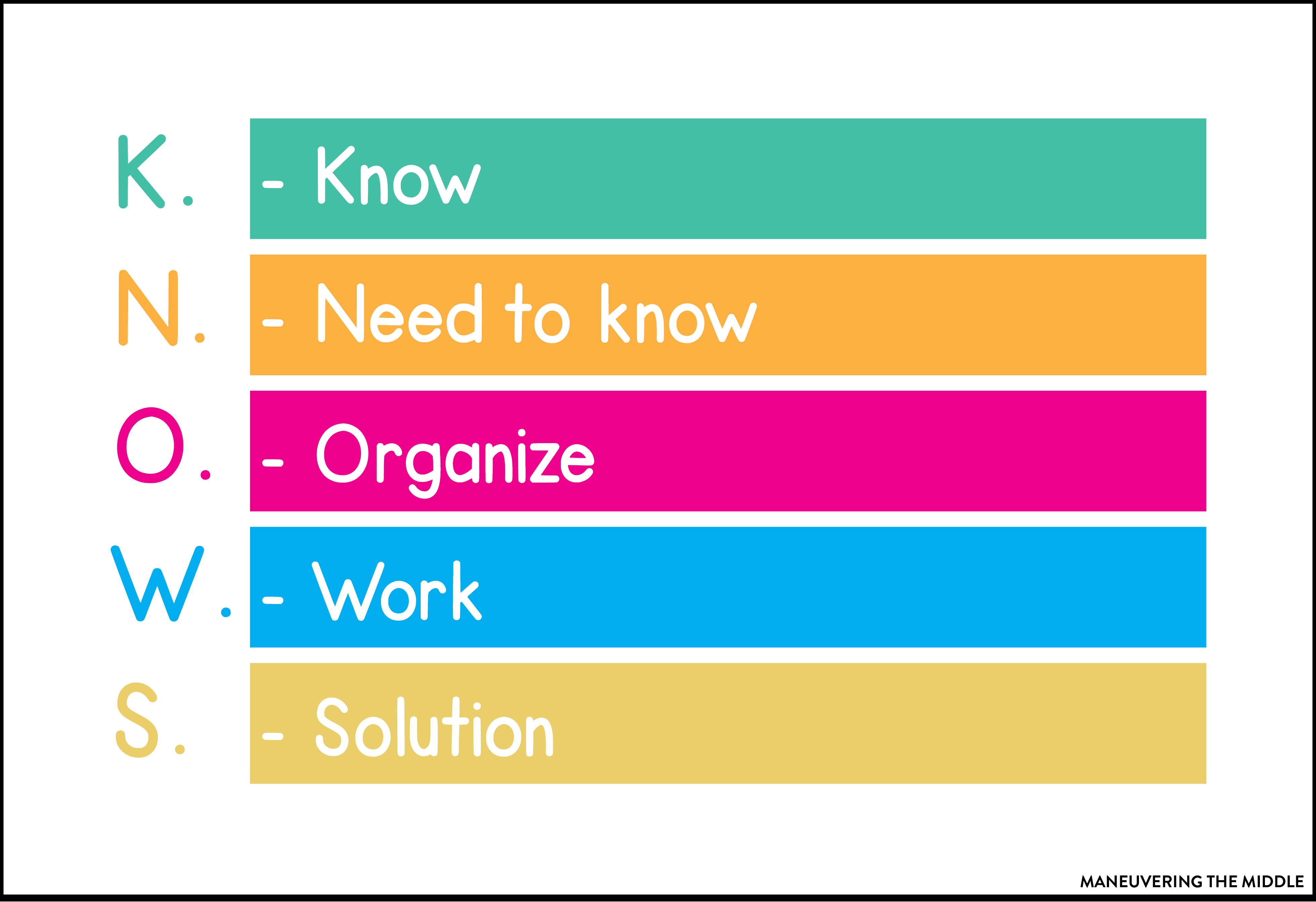
4. Maneuvering the Middle Strategy AKA K.N.O.W.S.
Here is the strategy that I adopted a few years ago. It doesn’t have a name yet nor an acronym, (so can it even be considered a strategy…?)
UPDATE: IT DOES HAVE A NAME! Thanks to our lovely readers, Wendi and Natalie!
- Know: This will help students find the important information.
- Need to Know: This will force students to reread the question and write down what they are trying to solve for.
- Organize: I think this would be a great place for teachers to emphasize drawing a model or picture.
- Work: Students show their calculations here.
- Solution: This is where students will ask themselves if the answer is reasonable and whether it answered the question.
I have rolled this problem solving strategy out to students, and it went decently. When I provided the boxes (seen below) for them to fill out, I received no heavy sighs that I was forcing them to show their work.
I think the boxes made it clear that it was part of the required work – not something ‘extra’ I was wasting their time with.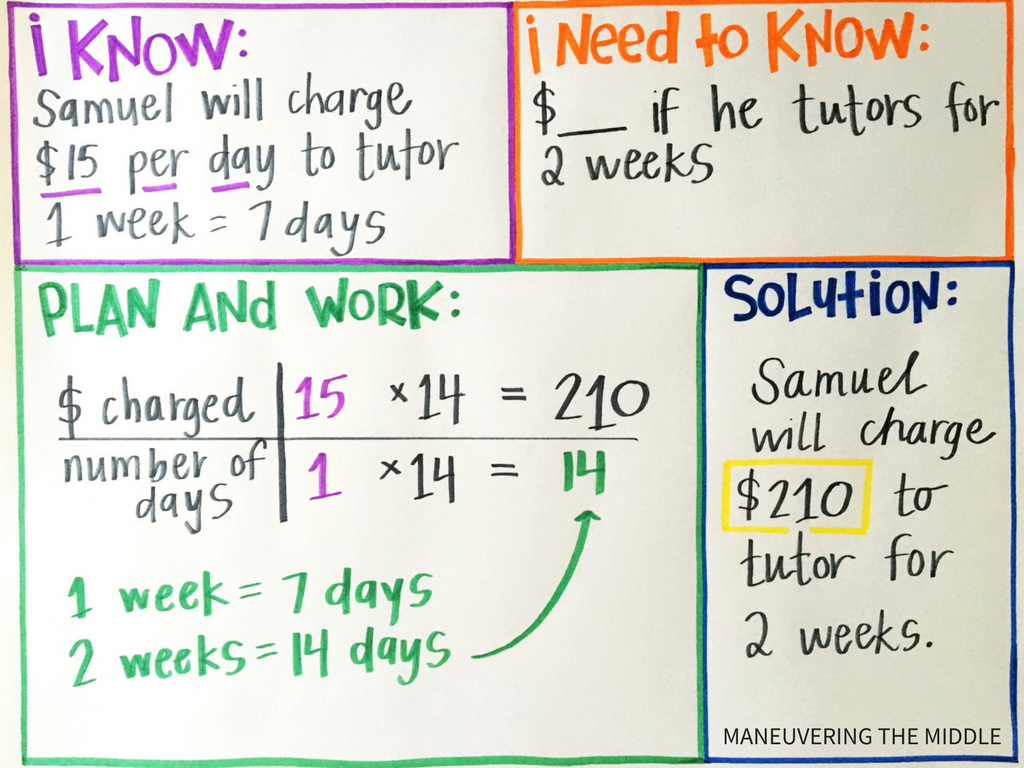
Ideas for Promoting Showing Your Work
- White boards are a helpful resource that make (extra) writing engaging!
- Celebrating when students show their work. Create a bulletin board that says ***I showed my work*** with student exemplars.
- Take a picture that shows your expectation for how work should look and post it on the board like Marissa did here.
Show Work Digitally
Many teachers are facing how to have students show their work or their problem solving strategy when tasked with submitting work online. Platforms like Kami make this possible. Go Formative has a feature where students can use their mouse to “draw” their work.
If you want to spend your energy teaching student problem solving instead of writing and finding math problems, look no further than our All Access membership. Click the button to learn more.
Students who plan succeed at a higher rate than students who do not plan. Do you have a go to problem solving strategy that you teach your students?

Editor’s Note: Maneuvering the Middle has been publishing blog posts for nearly 8 years! This post was originally published in September of 2017. It has been revamped for relevancy and accuracy.







As a reading specialist, I love your strategy. It’s flexible, “portable” for any problem, and DOES get kids to read and understand the problem by 1) summarizing what they know and 2) asking a question for what they don’t yet know — two key comprehension strategies! How about: “Make a Plan for the Problem”? That’s the core of your rationale for using it, and I bet you’re already saying this all the time in class. Kids will get it even more because it’s a statement, not an acronym to remember. This is coming to my reading class tomorrow with word problems — thank you!
Hi Nora! I have never thought about this as a reading strategy, genius! Please let me know how it goes. I would love to hear more!
Hi! I am a middle school teacher in New York state and my district is “gung ho” on CUBES. I completely agree with you that kids are not really reading the problem when using CUBES and only circling and boxing stuff then “doing something” with it without regard for whether or not they are doing the right thing (just a shot in the dark!). I have adopted what I call a “no fear word problems” procedure because several of my students told me they are scared of word problems and I thought, “let’s take the scary out of it then by figuring out how to dissect it and attack it!
Our class strategy is nearly identical to your strategy:
1. Pre-Read the problem (do so at your normal reading speed just so you basically know what it says)
2. Active Read: Make a short list of: DK (what I Definitely Know), TK (what I Think I Know and should do), and WK (what I Want to Know– what is the question?)
3. Draw and Solve
4. State the answer in a complete sentence.
This procedure keep kids for “surfacely” reading and just trying something that doesn’t make sense with the context and implications of the word problem. I adapted some of it from Harvey Silver strategies (from Strategic Teacher) and incorporated the “Read-Draw-Write” component of the Eureka Math program. One thing that Harvey Silver says is, “Unlike other problems in math, word problems combine quantitative problem solving with inferential reading, and this combination can bring out the impulsive side in students.” (The Strategic Teacher, page 90, Silver, et al.; 2007). I found that CUBES perpetuates the impulsive side of middle school students, especially when the math seems particularly difficult. Math word problems are packed full of words and every word means something to about the intent and the mathematics in the problem, especially in middle school and high school. Reading has to be done both at the literal and inferential levels to actually correctly determine what needs to be done and execute the proper mathematics. So far this method is going really well with my students and they are experiencing higher levels of confidence and greater success in solving.
Hi! Another teacher and I came up with a strategy we call RUBY a few years ago. We modeled this very closely after close reading strategies that are language arts department was using, but tailored it to math.
R-Read the problem (I tell kids to do this without a pencil in hand otherwise they are tempted to start underlining and circling before they read)
U-Underline key words and circle important numbers
B-Box the questions (I always have student’s box their answer so we figured this was a way for them to relate the question and answer)
Y-You ask yourself: Did you answer the question? Does your answer make sense (mathematically)
I have anchor charts that we have made for classrooms and interactive notebooks if you would like them let me me know….
Great idea! Thanks so much for sharing with our readers!
LOVE this idea! Will definitely use it this year! Thank you!
I would love an anchor chart for RUBY
I will definitely use this concept in my Pre-Algebra classes this year; I especially like the graphic organizer to help students organize their thought process in solving the problems too.
I love the process you’ve come up with, and think it definitely balances the benefits of simplicity and thoroughness. At the risk of sounding nitpicky, I want to point out that the examples you provide are all ‘processes’ rather than strategies. For the most part, they are all based on the Polya’s, the Hungarian mathematician, 4-step approach to problem solving (Understand/Plan/Solve/Reflect). It’s a process because it defines the steps we take to approach any word problem without getting into the specific mathematical ‘strategy’ we will use to solve it. Step 2 of the process is where they choose the best strategy (guess and check, draw a picture, make a table, etc) for the given problem. We should start by teaching the strategies one at a time by choosing problems that fit that strategy. Eventually, once they have added multiple strategies to their toolkit, we can present them with problems and let them choose the right strategy.
That’s brilliant! Thank you for sharing!
Mrs. Brack is setting up her second Christmas tree. Her tree consists of 30% red and 70% gold ornaments. If there are 40 red ornaments, then how many ornaments are on the tree? What is the answer to this question?
Whoops! I guess the answer would not result in a whole number (133.333…) Thanks for catching that error.
I used to teach elementary math and now I run my own learning center, and we teach a lot of middle school math. The strategy you outlined sounds a little like the strategy I use, called KFCS (like the fast-food restaurant). K stands for “What do I know,” F stands for “What do I need to Find,” C stands for “Come up with a plan” [which includes 2 parts: the operation (+, -, x, and /) and the problem-solving strategy], and lastly, the S stands for “solve the problem” (which includes all the work that is involved in solving the problem and the answer statement). I find the same struggles with being consistent with modeling clearly all of the parts of the strategy as well, but I’ve found that the more the student practices the strategy, the more intrinsic it becomes for them; of course, it takes a lot more for those students who struggle with understanding word problems. I did create a worksheet to make it easier for the students to follow the steps as well. If you’d like a copy, please let me know, and I will be glad to send it.
This is a supportive and encouraging site. Several of the comments and post are spot on! Especially, the “What I like/don’t like” comparisons.
Have you named your unnamed strategy yet? I’ve been using this strategy for years. I think you should call it K.N.O.W.S.
K – Know
N – Need
OW – (Organise) Plan and Work
S – Solution
Going off of your idea, Natalie, how about the following?
K now
N eed to find out
O rganize (a plan – may involve a picture, a graphic organizer…)
W ork
S ee if you’re right (does it make sense, is the math done correctly…)
I love the K & N steps…so much more tangible than just “Read” or even “Understand,” as I’ve been seeing is most common in the processes I’ve been researching.
I like separating the “Work” and “See” steps. I feel like just “Solve” May lead to forgetting the checking step.
I’m doing this one. Love it. Thank you!!
Hi,
I wanted to tell you how amazing and kind you are to share with all of us. I especially like your word problem graphic organizer that you created yourself! I am adopting it this week.
We have a meeting with all administrators to discuss algebra.
I am going to share with all the people at the meeting.
I had filled out the paperwork for the number line. Is it supposed to go to my email address?
Thank you again. I am going to read everything you ahve given to us.
Have a wonderful Tuesday!