Problem solving can be a challenge to teach. Perhaps, it is because we are trying to teach students to manage and implement a myriad of skills: thinking, observing, investigating, reasoning through situations, and accessing prior knowledge. Check out these strategies to get students thinking!
LISTEN ON: APPLE PODCAST | SPOTIFY
Problem Solving with Word Problems
In the book The Young Child and Mathematics, Juanita Copley states that problem solving happens through “doing, talking, reflecting, discussing, observing, investigating, listening, and reasoning.”
We can often mistake different methods for decoding word problems as problem solving skills. R.U.B.I.E.S. and C.U.B.E.S. and all of the acronyms where students are supposed to underline, box, or circle may feel productive, but they cannot produce the skills needed to solve real-world problems.
Why Are Problem Solving is so Difficult
There are a lot of different factors that play into this challenge and it could be a single isolated one or it could be a combination of several factors.
- Need for perseverance – some students can routinely go through all of the procedures involved in solving a math problem, but they haven’t yet acquired the perseverance needed to reason through a real-life situation
- Reading skills — tasks and real-world applications require reading comprehension and decoding skills to fully understand the situation and apply the mathematical reasoning skills necessary to solve
- Multiple steps — requires students to create a plan with several steps and work through the plan
- Incorrect vocabulary usage — when solving word problems, sometimes students have been instructed to primarily look for specific words like “per” “of” “each” “sum”…and then they attempt to apply the operation — but we know that doesn’t always work and can also over simplify the process.
Shift the Focus from the Answer
This post and video from Phil Daro (co-author of the CCSS) says that based on their studies, teachers need to shift the focus from answer-getting to sense-making. “When the answer is the only goal, genuine learning is undermined.”
He says that teachers put too much emphasis on the answers; answers are part of the process, but they are not the only learning outcome. That wrong answers are part of the learning outcome.
- Consider framing wrong “answers” as “discoveries.” If students reached a wrong answer, you talked more about why that approach doesn’t work instead of how to get the right answer.
- Consider giving students the answers before solving, removing some of the power, and instead spent class time figuring out different ways to get to the answer.
The goal of solving math problems is the critical thinking that happens along the way. Not the answer.
How do we teach problem solving?
Learning is not necessarily the solution to a specific question. We want students to apply sense-making to the rest of their lives.
I really want you to watch the video, but one of Daro’s suggestions is to provide students the correct answer before having students solve. It removes some of the power of finding the right answer, and puts an emphasis on figuring out different ways to get the answer. There are so many different ways to solve problems and it encourages students to think in this way.

Tip #1 – Allow flexibility in how students solve problems.
Showing your work is said so often that it can seem meaningless to a student. Give students options for ways they can show their work.
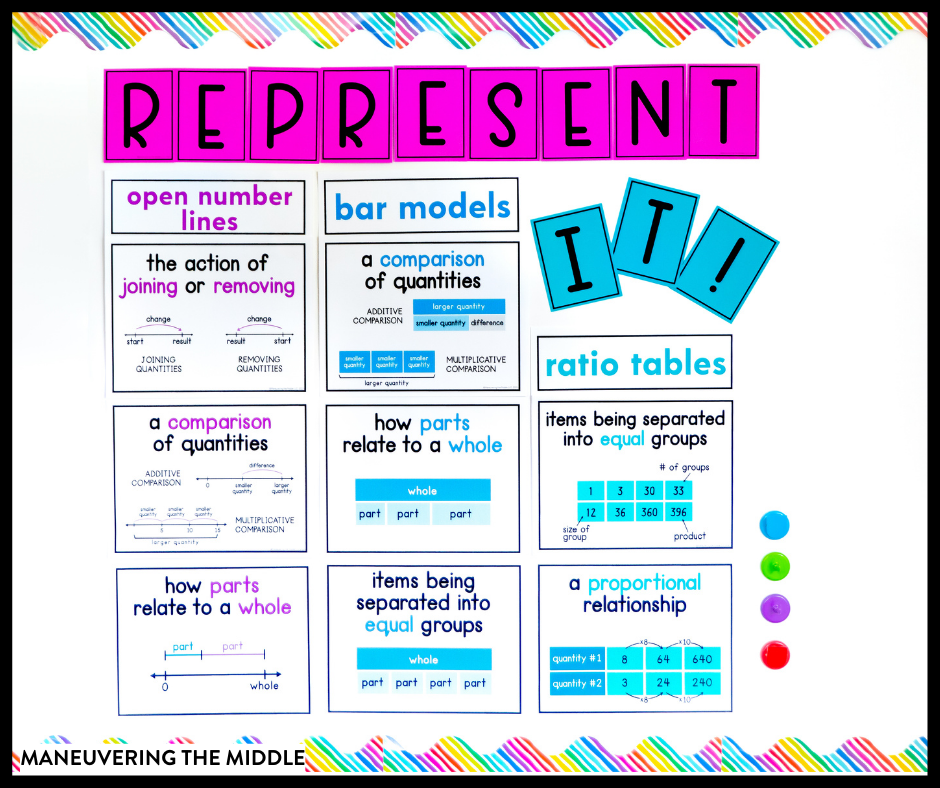
Grab a free REPRESENT IT bulletin board that will provide a visual aid for different ways to represent their work!
Here are a few examples:
- Write an equation
- Solve a simpler problem
- Draw a bar model
- Draw a picture
- Draw a graph
- Use an open number line
- Use manipulatives
- Guess and check
- Use logical reasoning
- Make a ratio table
Tip #2- Focus on quality over quantity.
Quality over quantity is going to mean different things for different teachers, depending on the number of students, the length of your class period and even the different concepts being covered. Here is one example for helping students focus on “sense-making” in a problem.
Let’s take this pretty basic word problem >> Mr. Roy overdrafts his account by $25.50 and then is charged a $10.35 fee by the bank. What is the change in Mr. Roy’s bank account?
Before modeling a think-aloud to discuss how to solve this problem (and move on quickly to the next), ask so many questions that students will have no choice but to THINK about what the problem is asking for. Shift the workload to the students. Here are a few I brainstormed:
- Who is Mr. Roy?
- What is an overdraft?
- Is a fee a good thing or bad thing? For who?
- Why is Mr. Roy charged a fee?
- What is the change measuring?
- Does he have more money or less money?
I just asked 6 questions and haven’t even gotten to the math yet! Model for students the type of critical thinking and questioning you want students to use when they are solving solo.

Then have students just try out the problem. Circulate to see the different methods. Come together to discuss the different ways you saw the problem solved.
Bring this problem to life by providing Monopoly money to students to “act” it out.
I love seeing students be problem solvers and I think it is such a lifelong skill that they will always carry with them. In fact, they may not frequently need to calculate the equation of a line or the probability of a compound event, but each and everyday they will use their “sense-making skills” to solve problems and make decisions.
If you want to focus on teaching problem solving, then All Access may be right for you!






Hi,
I really enjoy how thorough your blog is, especially this part on teaching students word problems. The blog is informative. I enjoyed listening to it via spotify. Thank you for linking additional resources!