If you haven’t had a chance to read part 1 Teaching Factoring Trinomials, then go back and do that before reading anymore. Today we are going to discuss Factoring Polynomials with special cases.

Factoring Trinomials When A>1
I hesitated to put a>1 in this blog post since it isn’t necessarily a special case, but I considered that you probably would teach this AFTER you teach factoring trinomials when a=1.
Let’s dive in!
Double check that there isn’t a GCF that can be factored out the a, b, c terms.
The AC method is a great way to teach your students how to factor. Explaining this method through text is hard to follow (I tried), so again, I am going to pass it to Sara to teach you how to factor trinomials when a>1.
Insert video here
If you love this video, then check out All Access, our curriculum membership that includes ~3 videos for every single lesson! She is also using the Student Handouts that are available in our Factoring Polynomials Unit.
Using the Box Method
The box method is excellent, and if you taught it when factoring trinomials when a=1, then there isn’t much new to cover. This video shows how to do this, but I also included a few graphics for you to reference.



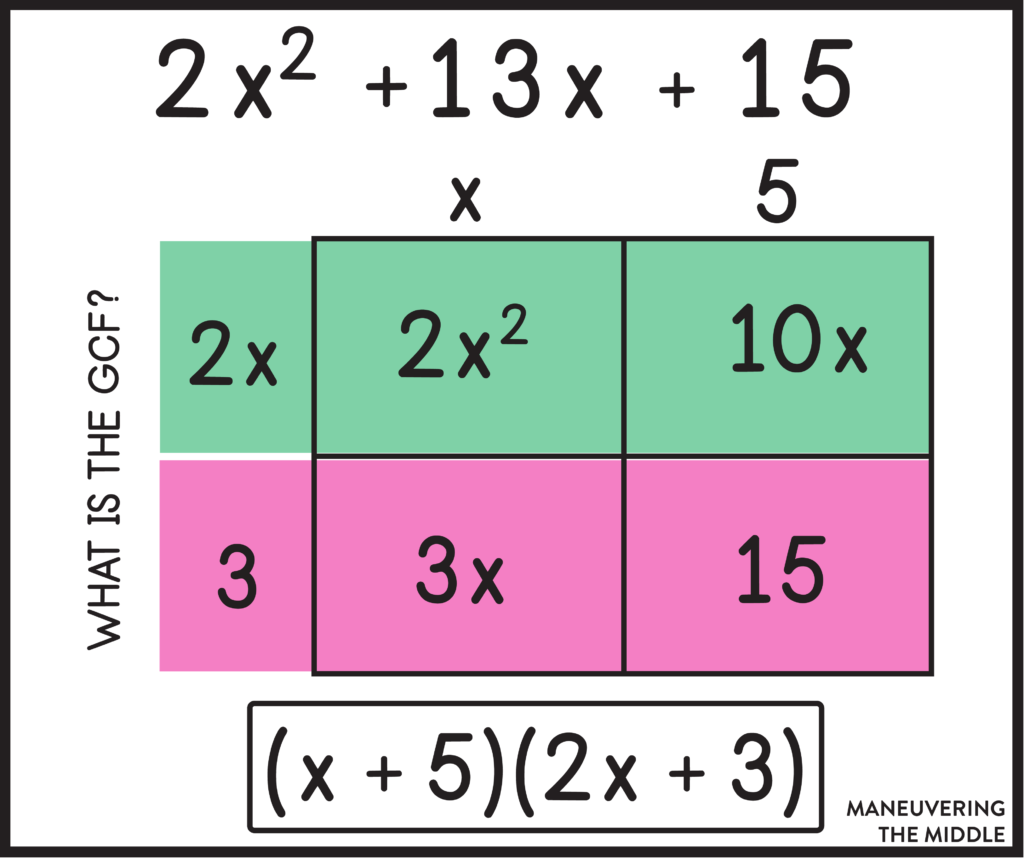
Factoring with Difference of Squares
I love difference of squares! We like to start by explaining how difference of squares exists. Let’s take x^2 -16. You can still ask your students, “What multiplies to -16 that also adds to 0?” Remember that b=0 in a difference of squares polynomial.

Forgive my repetitiveness, but remember that we still have to check to see if there is a Greatest Common Factor!
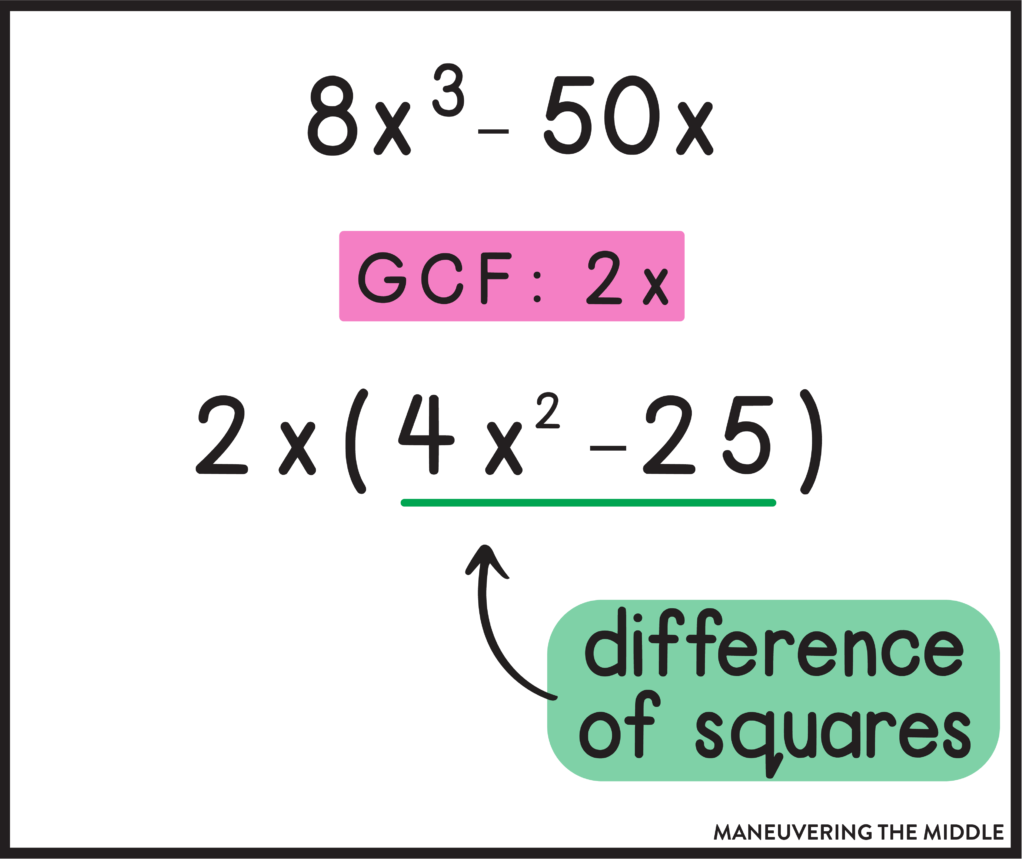
When I taught Algebra 2, we did Around the World or Head to Head Challenges using squares and square roots. I wanted students to internalize squares and square roots (for a multitude of reasons) but it served this skill very well. You may consider putting up an anchor chart so students have a visual.
Perfect Square Trinomials
By the time you are teaching perfect square trinomials, it is likely that students may have already factored a few perfect square trinomials. In fact, you don’t actually have to teach perfect square trinomials as a special case – it is helpful for students to recognize patterns, absolutely! Students can still factor these trinomials using the methods already taught!
Teaching students to recognize the form is helpful and will increase their proficiency in taking the square root of numbers.

How do you teach factoring trinomials and polynomials?






I also teach my Algebra II students the “tic tac toe” method. This is really just a visually organized way of using the AC method. There are a few videos on YouTube that illustrate the use of the “#” organizer.