Dividing fractions doesn’t have to be scary! I was shocked to learn that this study determined that students’ knowledge of fractions and division uniquely predicts their achievement in high school years later.
Make sure to grab your free how to teaching fraction division guide below
Check out the player to hear the interview, or you can read the transcript that has been edited for succinctness below.
Listen On: APPLE PODCAST | Spotify
Who is our expert on fractions?
To connect with Brittany and learn more, you can follow her on Instagram @mixandmath or check out her website Mix and Math.
Brittany Hege is a math educator who has worked with students and teachers in both upper elementary and middle grades. She holds a master’s degree in Elementary Mathematics Education and is passionate about helping teachers grow their understanding of the math they teach. Brittany believes in the power of experiencing math through hands-on work and uses her platform, Mix and Math, to equip upper elementary teachers with the knowledge, resources, and confidence to inspire a generation of empowered math learners.
Why are students and teachers fearful of fractions?
Similar to multiplication facts, fractions are where students decide if they love math or hate math. Typically, fractions are taught very procedurally. There are many rules and procedures to memorize, and when students struggle, they lose their confidence.
Teachers carry their own learning experience with fractions into their teaching. Just like students, teachers can also fear fractions. And if we have taught fractions, and the lesson bombed, it reinforces the idea that fractions are something to just get through.
How do students overcome this fear of fractions?
It starts with teachers. Confidence in teaching a concept comes from understanding the concept. When teachers take the time to really understand fractions, it grows their confidence and then builds students’ understanding.
Teachers have to make fractions concrete by making fractions hands-on.
- What does this fraction actually mean?
- What does it look like in real life?
- How do we operate in a concrete way?
What is the progression of fractions in elementary school?
Fraction understanding begins in 3rd grade. In 4th grade, students start operating with fractions, but the standards focus on conceptual understanding, not the algorithm. In 5th grade, students should be able to understand fraction division and what it looks like in the real world. By 6th grade, students are expected to divide fractions by using the standard algorithm.
When students come into middle school with gaps in their knowledge of fractions, teachers typically drill and kill the procedures because they feel the urgency to fill the gaps so that they can move onto their grade-level content.
Why should we integrate models into our teaching?
Models help students visualize; models show what a fraction looks like and what the operation actually means.
What does 2.5 times ¼ actually mean? If students don’t have context or hands-on experience, they don’t realize that this number sentence means two groups of ¼ and ½ of ¼.
For a teacher who did not learn it that way, it can be intimidating. The best thing a teacher can do for their students is to grow their own content knowledge and to grow their own understanding.
We cannot change everything about the way we teach in one year. Fractions would be a good place to start. Get into a community like a Facebook Group and ask other teachers how they would teach it.
What are the two different types of division?
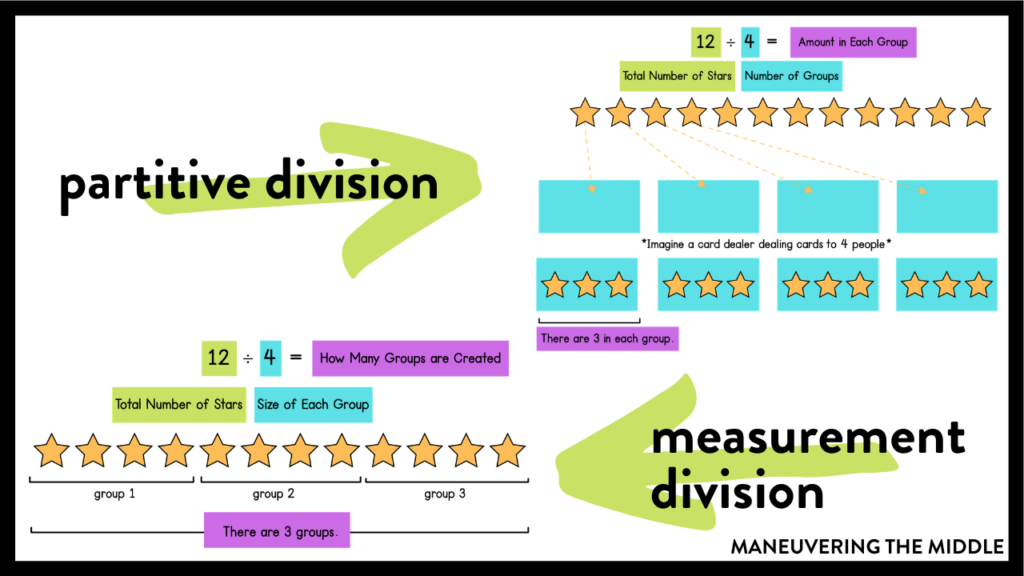The two types of division are fair share and measurement.
Fair share (or partitive) division means to divide an amount into a given number of groups, and we want to know how much is in each group.
Whole Number Example: I have $12, and I want to give 3 kids the same amount. How much money does each kid get?
Fraction division example: I have ¼ of a cookie and I want to share it with 2 friends. What fraction of the cookie does each friend get?
Measurement (or repeated subtraction) division means to divide evenly into groups of a given size.
Whole number example: I have $12, and I want to give each kid $4, how many kids can I give money to?
Fraction division example: I have 2 cups of flour. Each cupcake requires ¼ cup of flour. How many cupcakes can I make? So we are measuring it out – ¼ cup and another ¼ cup and another until we reach 2 cups of flour.
Measurement division is typically how we see fractions divided in middle school, but students may not understand that that is a division problem. Students also cannot determine if their answer is reasonable because they do not know the action behind it. In elementary, students learn that division makes numbers smaller, so it can be confusing to students when 2 divided by ¼ equals 8.
DIVE DEEPER BY GRABBING YOUR HOW TO TEACH DIVIDING FRACTIONS FREEBIE
For a better viewing experience, please download the guide and open in Adobe Reader or Preview.
To connect with Brittany and learn more, you can follow her on Instagram @mixandmath or check out her website Mix and Math.
How do you teach dividing fractions?
