Do your students often make mistakes using the standard multiplication algorithm? Then this post is for you! Here are 5 alternative multiplication strategies for your upper elementary and middle school students.
1. Open Area Model
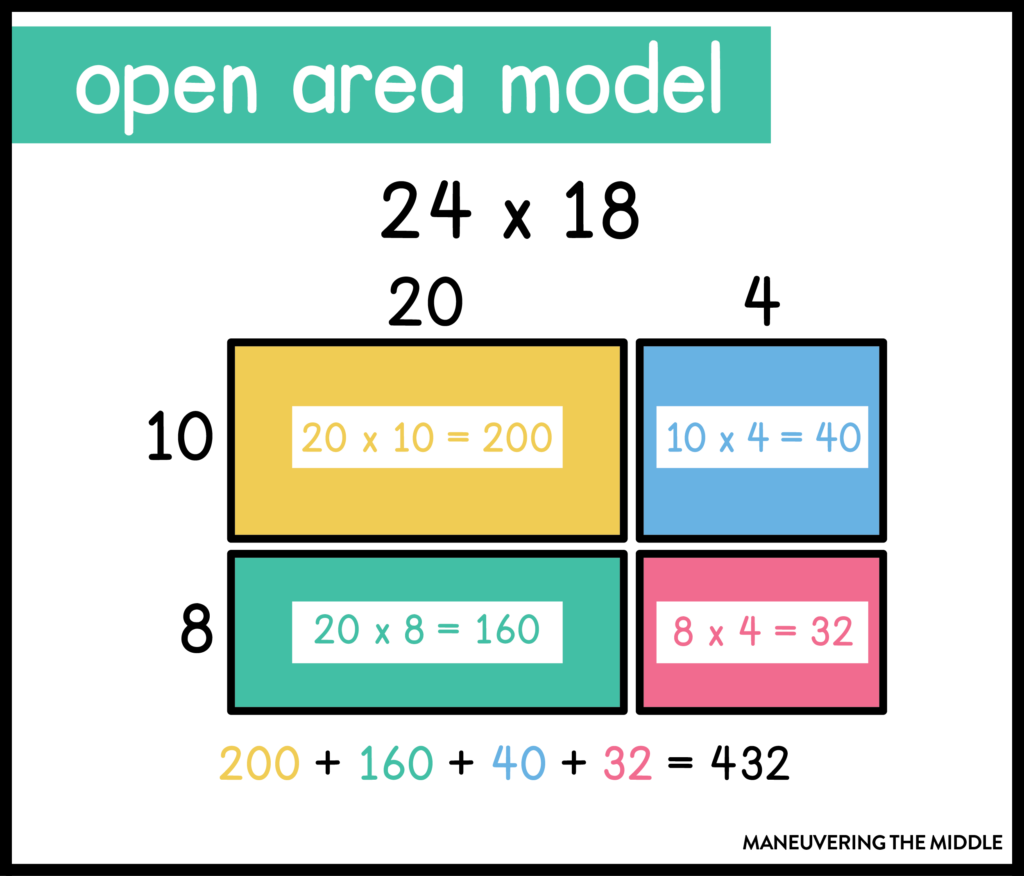
The area model demonstrates that when multiplying two numbers, you can find partial products and add them together to find the overall product. The open area model is my favorite alternative multiplication strategy and where I would start. After your students understand the basics of an array, the open area model is the next best model for students to fully see what is happening conceptually when multiplying (especially when multiplying 2 digits times 2+ digits).
The steps are already built in. They know that each box needs to be filled in. This keeps students organized and (hopefully) more accurate.
Additional benefits: this format will help students in high school Algebra multiplying and dividing polynomials.
2. Partial Product Multiplication
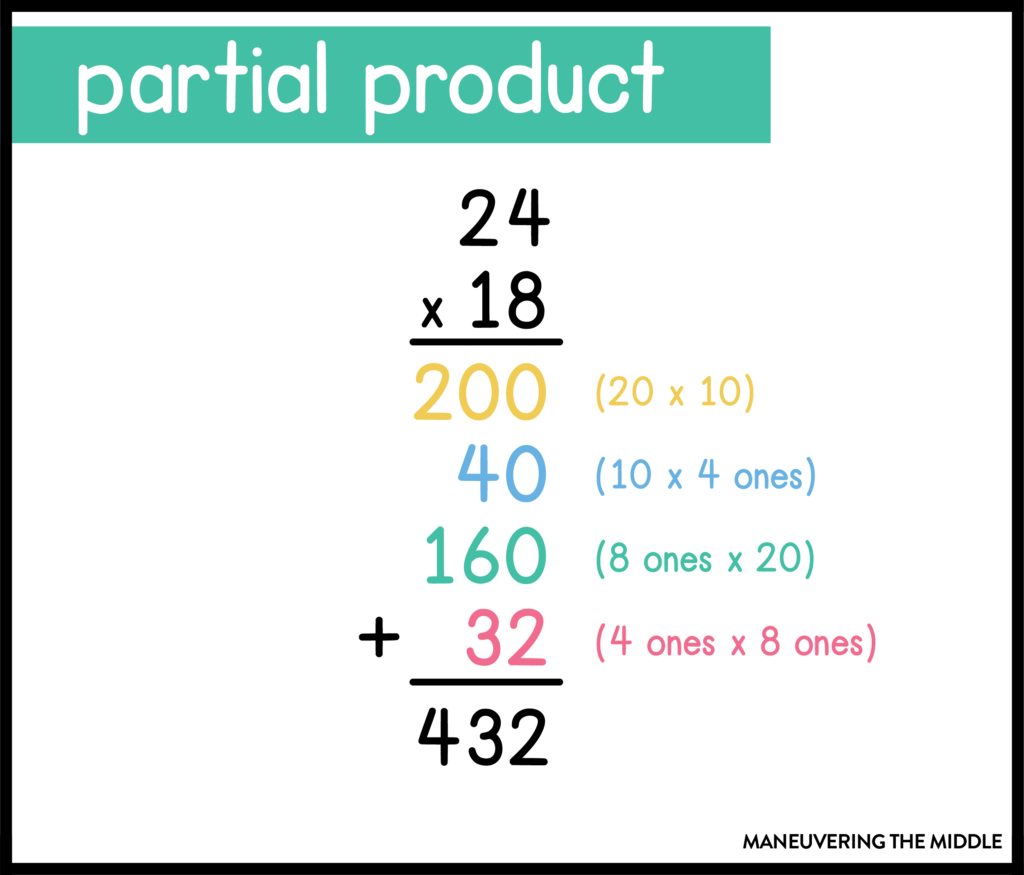
Partial product multiplication is the open area model without the boxes. Essentially, students are completing the exact same steps in the same order, but without the array format. While I wouldn’t start here, I think reinforcing the open area model with a partial product number sentence is the perfect progression.
3. Distributive Property

Using the distributive property is a multiplication strategy that will later reinforce another important math skill. Have students break down one of the factors into its expanded form and then multiply.
4. Chunking Using a Ratio Table
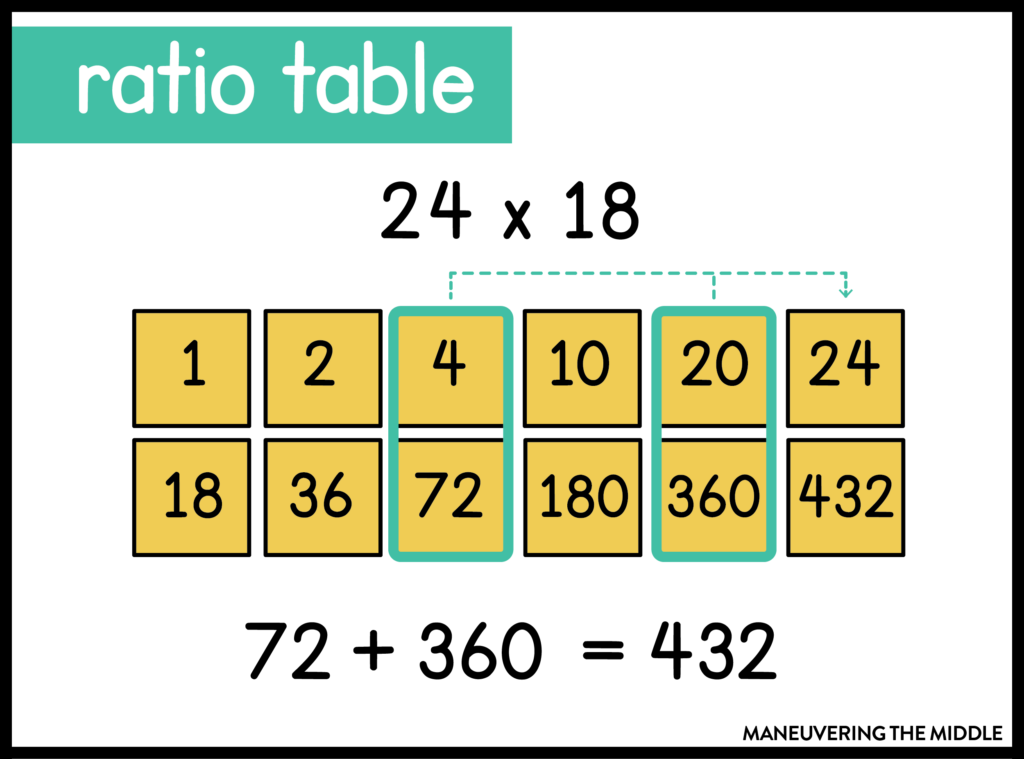
You can use a ratio table to split a factor into chunks (in this case 24 was broken down into 4 and 20) to find partial products that are then added together to find the final product. Have students take advantage of friendly math like doubling and multiplying by 10.
5. Over and Under
In order to use friendly numbers, multiply by more (or less) groups than necessary. Then, subtract the extra groups, or add the missing groups.
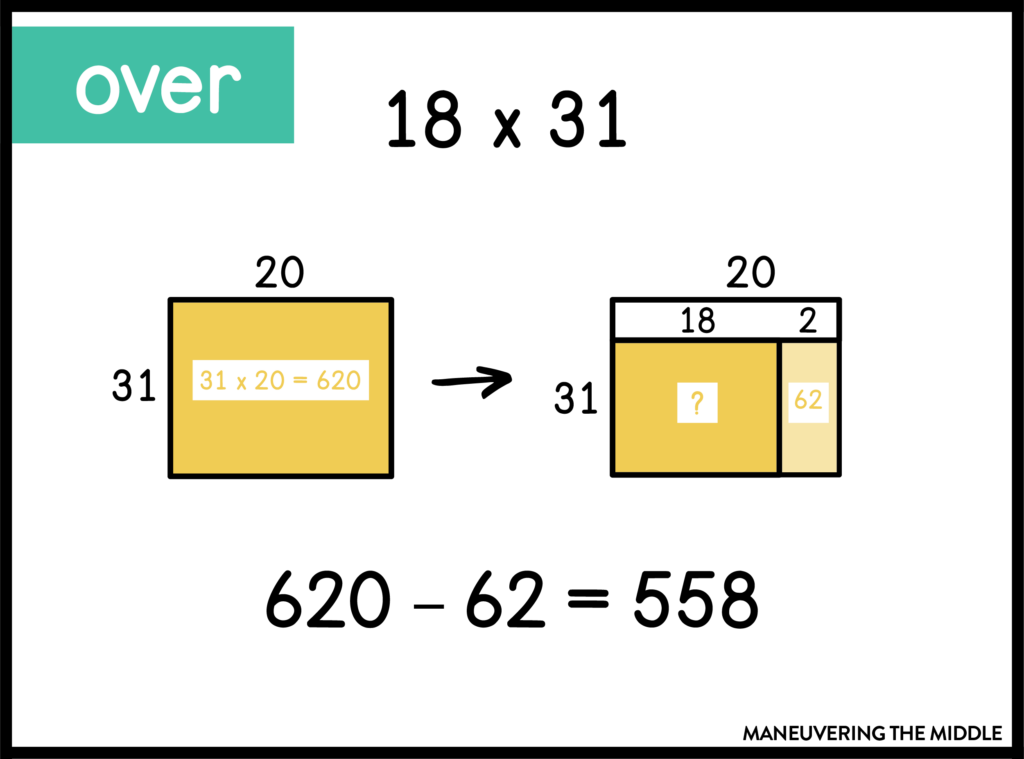
In this example, I traded 18 for 20. After finding the product of 31 and 20, I found the product of 31 and 2 (since 20 – 18 = 2). I subtracted this product of 62 from 620 to find the answer to our original problem 18 x 31.
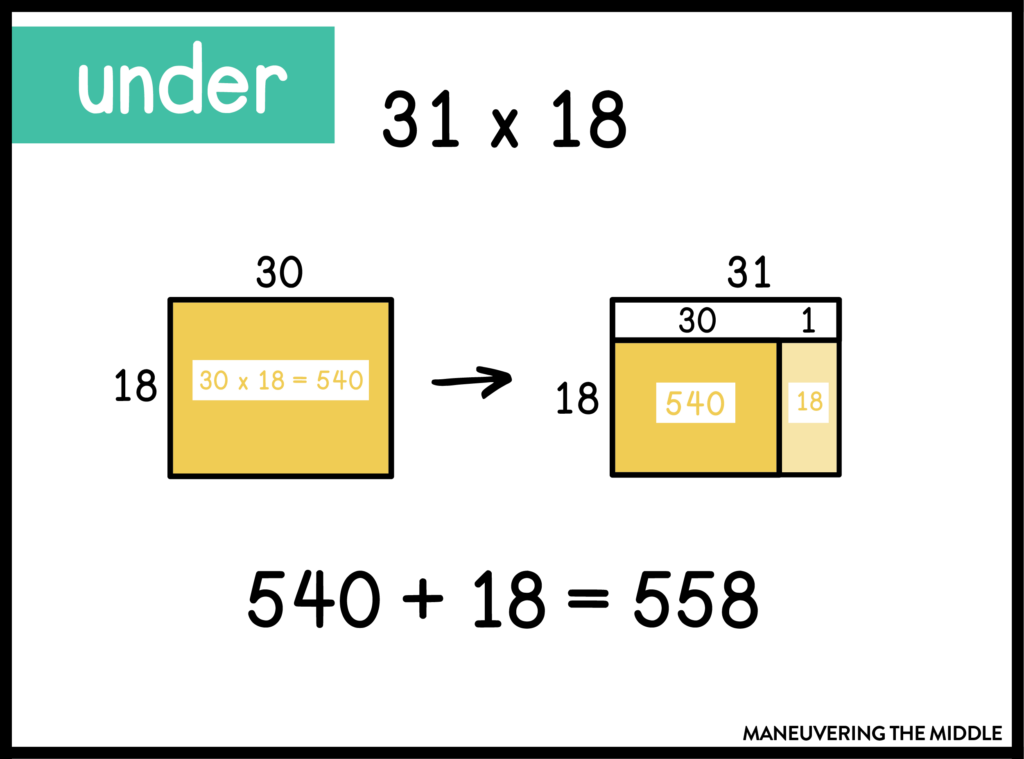
In this case, I shot under by trading 31 for 30. I knew I would be missing one group of 18 so I added that to the product of 30 and 18.
What multiplication strategy is your favorite? Interested in more multiplication posts, check out our posts on Multiplication Facts and the Distributive Property.
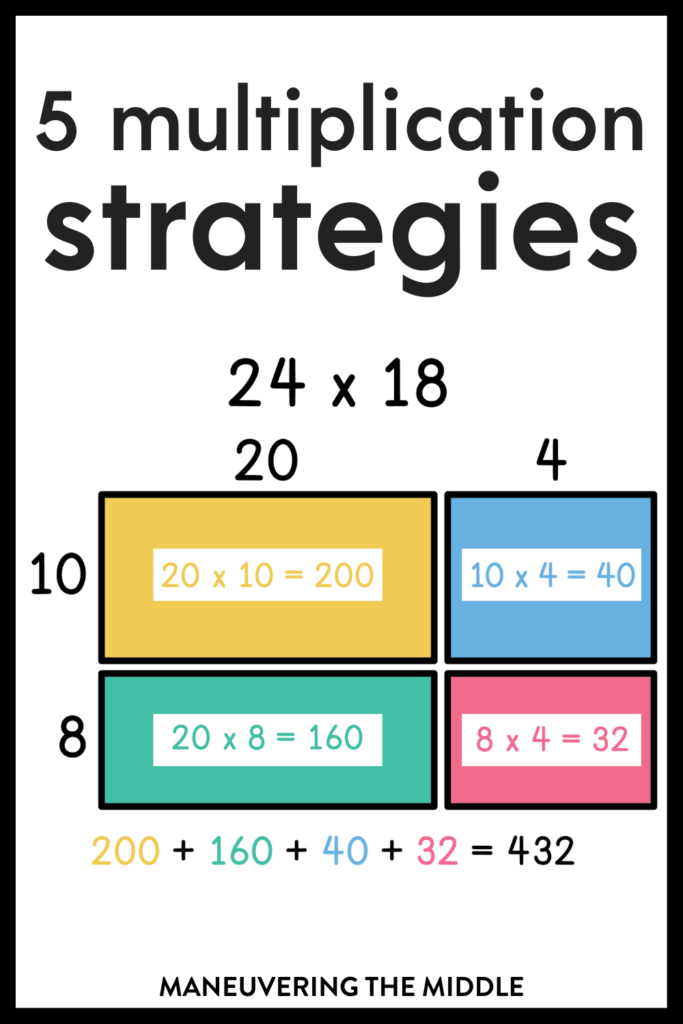


I love how you presented so many different strategies so that all learners have a choice that works for them. Saving this for later, it will be great to reference during small group instruction for students struggling with multiplication!