Making Algebra Relevant

In my years of teaching, I had the opportunity to teach Algebra 1 as an on-level course for 9th grade freshman and as a pre-AP course to 8th grade students.  While the two ages and settings (middle school vs. high school) differed, the content remained much the same. As a math teacher, Algebra 1 is the definition of fun!  For me, all of the pieces come together, and you have the opportunity to see it “click” for your students. For some students, they can begin to see a disconnect between algebra and the “real world” — enter the question, “When are we going to use this?” 

They have a point.  Not everything that you learn in Algebra 1 is going to directly translate to your career — you may not graph systems to determine the solution, but you may be comparing two different services and want to know which one is a better value.  Algebra 1 does teach you how to reason, how to think abstractly, and how to apply problem solving skills. So, how can we as teachers go about making algebra relevant?

I also want to note that often Algebra 1 is not the gateway subject; it’s the gatekeeper.  Future success in math (and arguably the rest of a student’s education) is reliant on success in the foundation of algebra.  Statistics are not friendly to those who fail Algebra 1.  By making it more relevant and by showing the connections to the real world, students are more likely to be engaged and participatory and, thus, are more likely to be successful!

1. Make Connections to the Real World

We’ve all seen this meme before.  Real-world math problems can be a little silly.  I personally believe that the sillier it is, the better.  (Click to see how I liked to handle funny word problems in my classroom.)

However, when we can connect using algebra to solve interesting, REAL real-world problems that are happening right now, we engage students who wouldn’t otherwise be engaged.  This is a great website with different and interesting problems for students to consider. They are sorted by grade level, and I found myself clicking each one just out of sheer interest for the topic (not the math!).

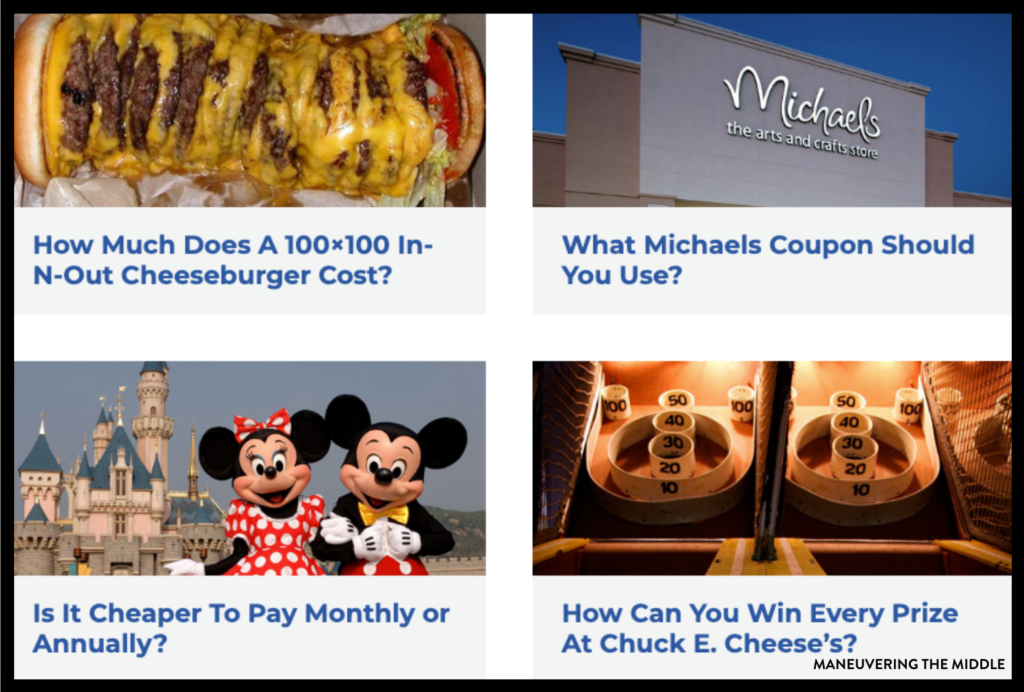
Here are just a few of the examples — 

2. Tailor curriculum to students’ interests

This article is fascinating. Essentially, studies show that students are more successful in math when the curriculum factors in their personal interest. 

“In the study, half of the students chose one of several categories that interested them — things like music, movies, sports, social media — and were given an algebra curriculum based on those topics.  The other half received no interest-based personalization… Walkington found that students who had received interest-based personalization mastered concepts faster.” 

Later in the study, she removed the interest-based personalization to see if the concepts were retained over time.

“‘Students that had previously received personalization, even though it was gone, were doing better on these more difficult problems as well,’ said Walkington.”

And for the students who were already struggling with algebra? Making algebra relevant will serve your struggling students the most.

“‘We picked out the students who seemed to be struggling the most in Algebra I, and we found that for this sub-group of students that were way behind, the personalization was more effective,’ Walkington said.”

UPDATE: ALGEBRA I DIGITAL ACTIVITIES ARE NOW AVAILABLE!

3. Incorporate Project-Based Learning

When students engage in a process to solve a real-world problem or to answer a complex question, they are taking ownership of their learning.  Project-based learning supports my last two points, but more than that, it makes the topic’s relevance more tangible than the typical worksheet.  Organizing information, solving a problem, and presenting a solution to peers are things that many students will need to be able to do in the real world, even if they don’t involve math.

4. Focus on the thinking, not just the process

Conceptual learning vs. procedural learning: For too long I focused on communicating what steps to take solving problems rather than having students explore what steps to take and WHY those steps are taken.  Let’s take solving systems of equations. There can be MANY steps to solve a systems problem by graphing, elimination, or substitution, and MANY students will solve these problems without really understanding what these types of problems represent.  If students do not understand that the purpose of a systems problem is to find the break-even point in two situations, then there was a missed opportunity to connect algebra’s relevance to their lives.

What are some of the ways you make algebra or math relevant in your classroom?