Let’s discuss strategies for teaching math concepts using the CRA framework. Remember that the CRA framework has proven to help students grasp difficult math concepts. If you are scratching your head asking yourself, “What is the CRA framework?” be sure to go back and read this post.

What is the CRA?
I like this definition best. “The CRA is a three-stage learning process where students learn through physical manipulation of concrete objects, followed by learning through pictorial representations of the concrete manipulations, and ending with solving problems using abstract notation.”
ROUTINES AND PROCEDURES
How do we set students up for success when using manipulatives?
- Tell students the purpose of using manipulatives. Explain how it is foundational to their success in math and how it is something you want to be able to trust your students with.
- Tell students WHAT TO DO. Telling students what to do is better than telling them what not to do. Example: manipulatives stay on the dry erase mat versus don’t throw manipulatives.
- Have students clear their desks of computers, binders, or anything else that can obscure your view of how the manipulatives are being used.
- Assign a materials manager as a group role. This student is responsible for making sure their group is using the manipulatives correctly and that they all get returned.
- Build in time for cleanup! If you are using manipulatives or any extra type of supply, give yourself lots of extra cushion at the end of class for clean up. Make sure to use a timer to encourage speed.
- If you want to minimize the number of manipulatives out at a time or you don’t have a whole class set of manipulatives, use a station or small group table for the manipulatives. This will narrow down the materials to manage to one area of the classroom and a smaller set of students.
- Remember, the more practice students have using manipulatives, the better they will get at cleanup and using them responsibly.
BEST PRACTICE #1: LET STUDENTS EXPLORE
There are 2 things you will have to balance as you model for students – the conceptual understanding piece with the procedures of using the manipulatives, but also I would encourage adequate exploration time. Exploration time can be really meaningful if you have strong and planned questions to guide your students’ thinking.
In this post, I wrote about not taking opportunities away from students to think. Sometimes demonstrating exactly what to do removes any of the thinking for students. It makes them follow a procedure to the T, which doesn’t allow for flexibility in their thinking.
Here is an example of how you can give students time to grapple with the content without modeling exactly what to do for them.
Let’s consider adding integers. Conceptually, students will need to understand that one side of the counter and its color represents negative and the other side represents positive. Students will also need to understand negative and positive numbers value in relation to zero. Perhaps, students can discover zero pairs without your explanation?
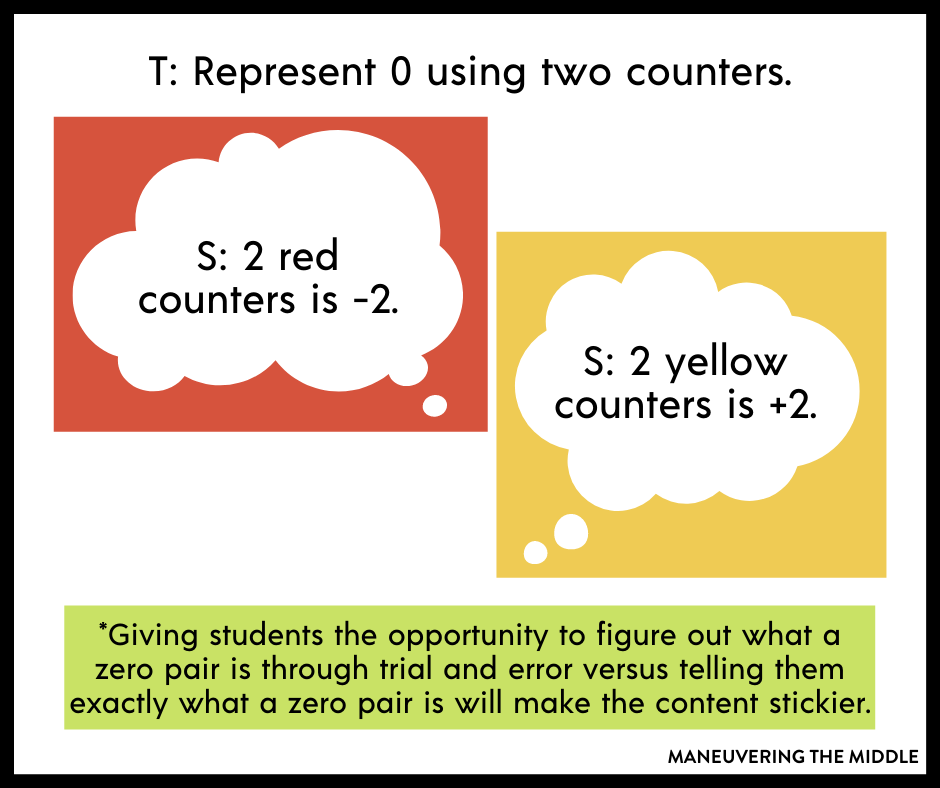
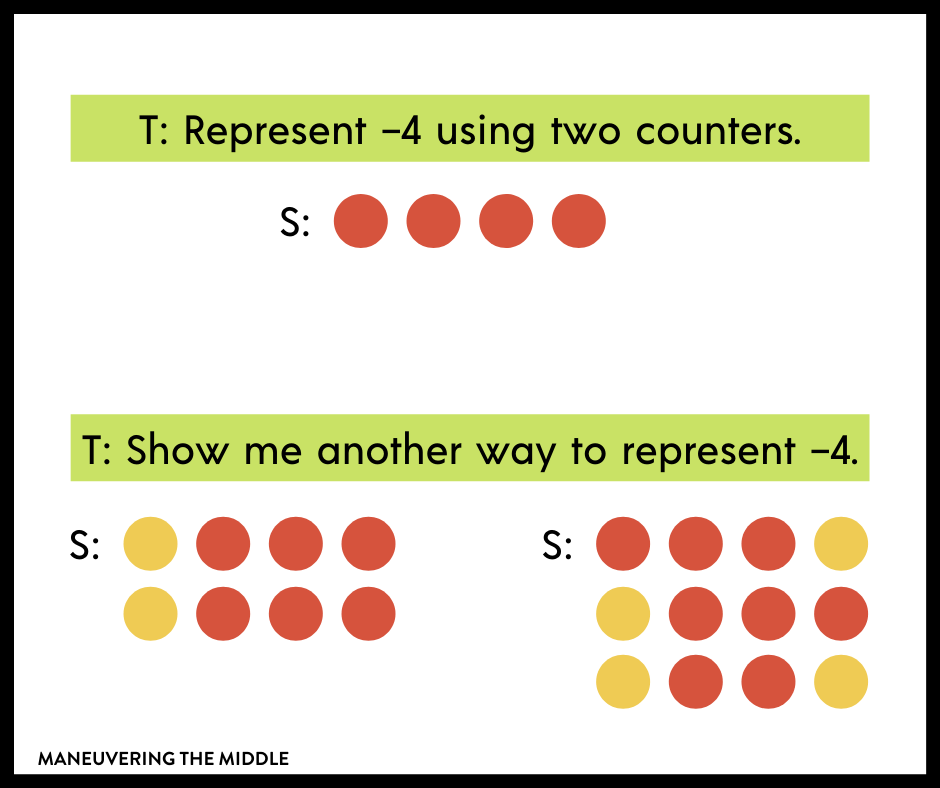
Now this will not always work with more complex situations, but I think with proper scaffolding and questioning, you should give students the opportunity to try something before showing them the exact procedure for working with the concrete representations.
BEST PRACTICE #2: Pair Manipulatives and Representations with the Abstract
“Explicit instruction that involves the use of manipulatives should also include the presentation of the numerical problem (Miller, Stringfellow, Kaffar, Ferreira, & Mancl, 2011).”
This study makes a great point. Students need to connect the manipulatives to the abstract as they are working, which means as they are working with the manipulatives, they need to be writing down what they are doing as they solve.
For example, when a student is using algebra tiles, connecting that the physical removal of two tiles from each side of the equation is the same thing as writing down “-2” on both sides of the equal sign will build that deeper understanding. We want students to understand WHY they are doing something.
Be sure to grab our freebies for Getting Started with Algebra Tiles.
The best part of the CRA method is how students will internalize the process. Some students will arrive at the abstract and never look back. Other students will draw models to support their thinking, while some students will request using a set of manipulatives well after you have taught the algorithm. That is the beauty!
Continue to spiral these concepts throughout the year using the different parts of the framework. If you go over the concrete and the representational on one day and then spend the entire year using the abstract to solve equations, then chances are your students will do the same thing too.
WHEN AM I GOING TO HAVE TIME TO DO THIS?
If you are already feeling very stretched with your scope and sequence, here are my thoughts:
Many times our scope and sequences allow some time for reteaching when the students do not master the concepts. Consider that by spending time building the conceptual understanding using concrete and pictorial representations, that you may not need the extra time for reteaching.
You can teach the concept in tandem using the manipulatives. If you are already going to spend time teaching math, you may as well introduce tools that will support student understanding.
“Students who use concrete materials develop more precise and more comprehensive mental representation, often show more motivation and on task behavior, understand mathematical ideas, and better apply these ideas to life situations.”
“Students are more apt to gain and retain an understanding of math concepts when they are taught using CRA.”
These two quotes from this study are the positives seem to outweigh the negative of being a little bit behind. Developing these foundational skills will only benefit students in the long run.
What are your strategies for teaching math concepts?