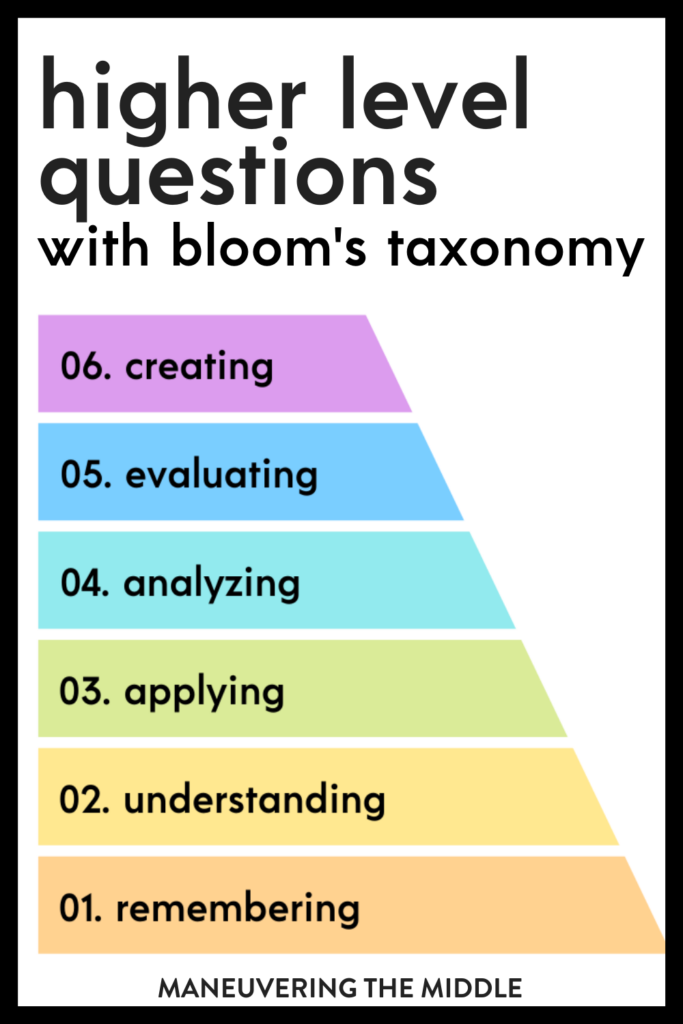
Higher level thinking is a goal for many teachers. Students retain knowledge when they have thought deeply about it. And in order to get our students to think at a deeper level, we have to be asking questions that require them to access those parts of the brain.
Encouraging higher level thinking is so interconnected to your classroom culture, the rigor of your content, and then of course the types of questions you are asking. Then we get into the challenges of collecting your students’ thinking – are they answering verbally or on paper? Can you give feedback quickly?
It makes sense that would be the case. If the whole entire goal of education is to provoke thought, then of course there would be so many facets of instruction connected to it.
This post is part 2 in our Instructional Design Series. Check out Unpacking Math Standards and the CRA framework. And if you haven’t grabbed our lesson planning template yet, make sure to grab it down below.
LISTEN ON: APPLE PODCAST | SPOTIFY
THE PROBLEM
The purpose of questioning in our classrooms:
- Questions give us feedback on what and how our students are processing and internalizing their learning.
- Questions also can be used to guide student thinking.
If you are asking questions throughout class and then students are struggling on the assessment, it’s possible that your questions in class are not aligned to that which a student is expected to do on the assessment.
Peter Lijedahl touches on this a bit in his book Building Thinking Classrooms, where he talks about “studenting”. Doing behaviors that look productive, “filling in notes or mimicking the teacher” but they aren’t actually reasoning their way through the problem.
We can make some small adjustments to the questions and interactions in our classroom to build those thinking muscles.
Building a Strong Classroom Culture
For students to think and answer questions at a higher level, we want students to be comfortable with making mistakes.
Phil Daro (co-author of the CCSS) says that teachers put too much emphasis on the answers; answers are part of the process, but they are not the only learning outcome. That wrong answers are part of the learning outcome.
What if you framed wrong “answers” as “discoveries”? If students reached a wrong answer, you instead talked more about why that approach doesn’t work instead of how to get the right answer.
The Questions You Are Asking
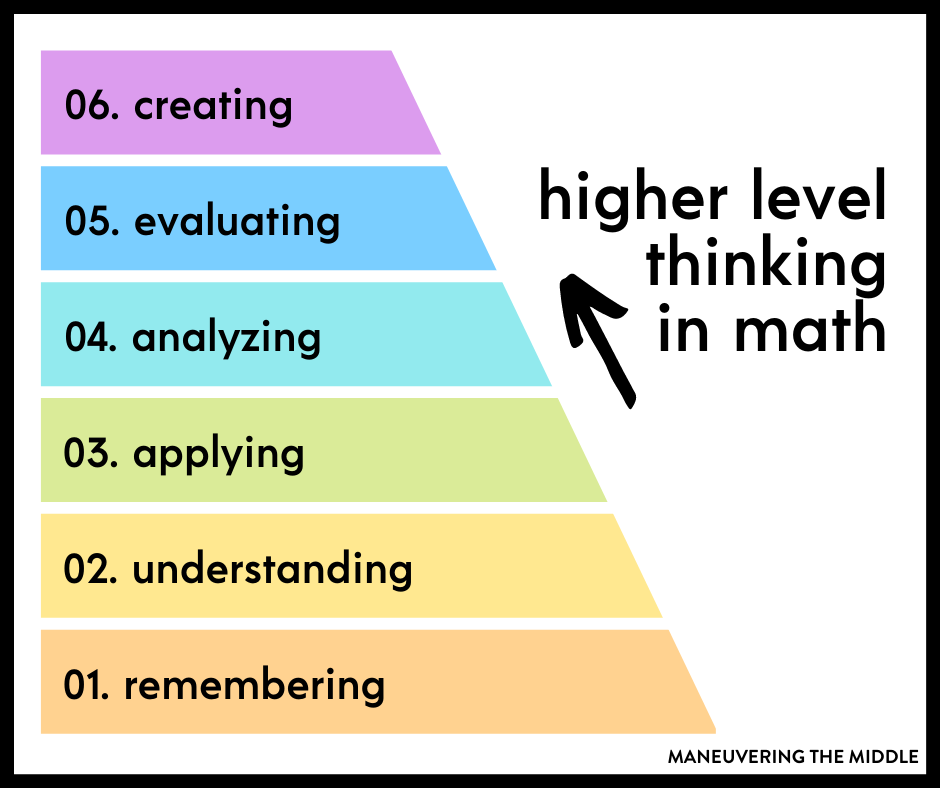
If we are focusing on higher level thinking using higher level questions, we have to focus on the types of questions we are asking.
To do this, I am going to refer to Bloom’s Taxonomy which is a hierarchy of learning objectives that rank lower order thinking skills to higher order thinking skills.
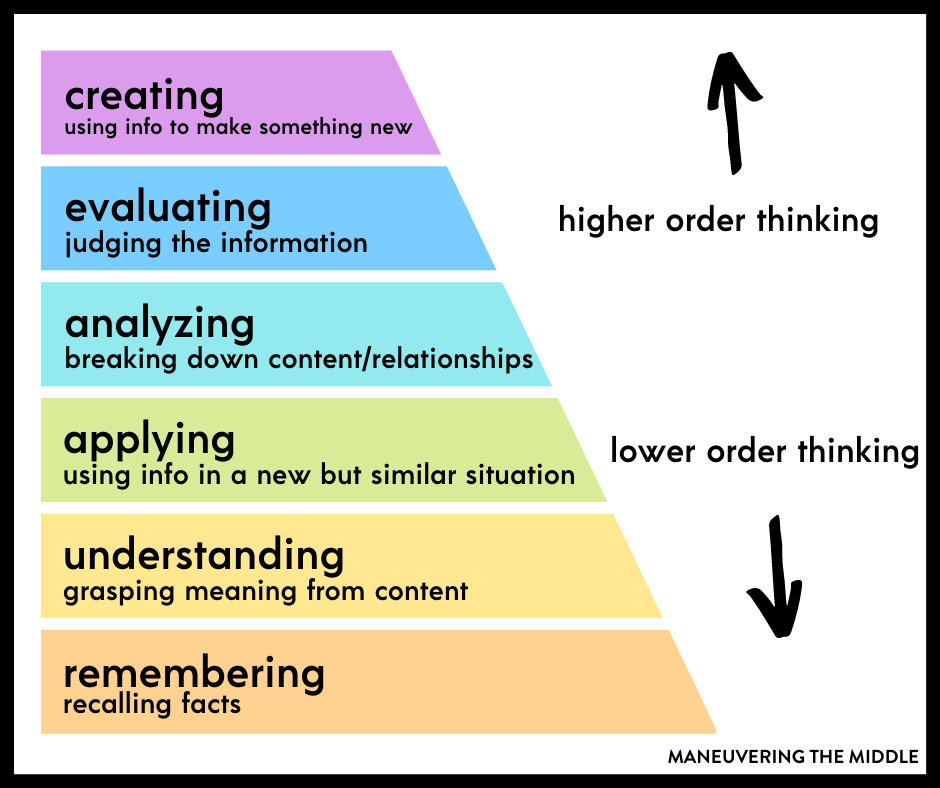
Now remember this is a pyramid, so those lower levels have a purpose and provide a foundation. These are the easy questions to ask, the ones that just roll off the tongue and don’t really require much forethought.
In math it sounds like – “What do we do next?” “What is the solution?” “What operation will we use?”
The higher level thinking questions are those that take a little more forethought and planning. These are the questions that require students to analyze the relationships in a process or make an evaluation on how to approach the problem based on given information.
One of the easiest ways to elicit higher level thinking is to teach students multiple approaches to a specific concept and then have students evaluate and justify why one process may be better than another based on given information.
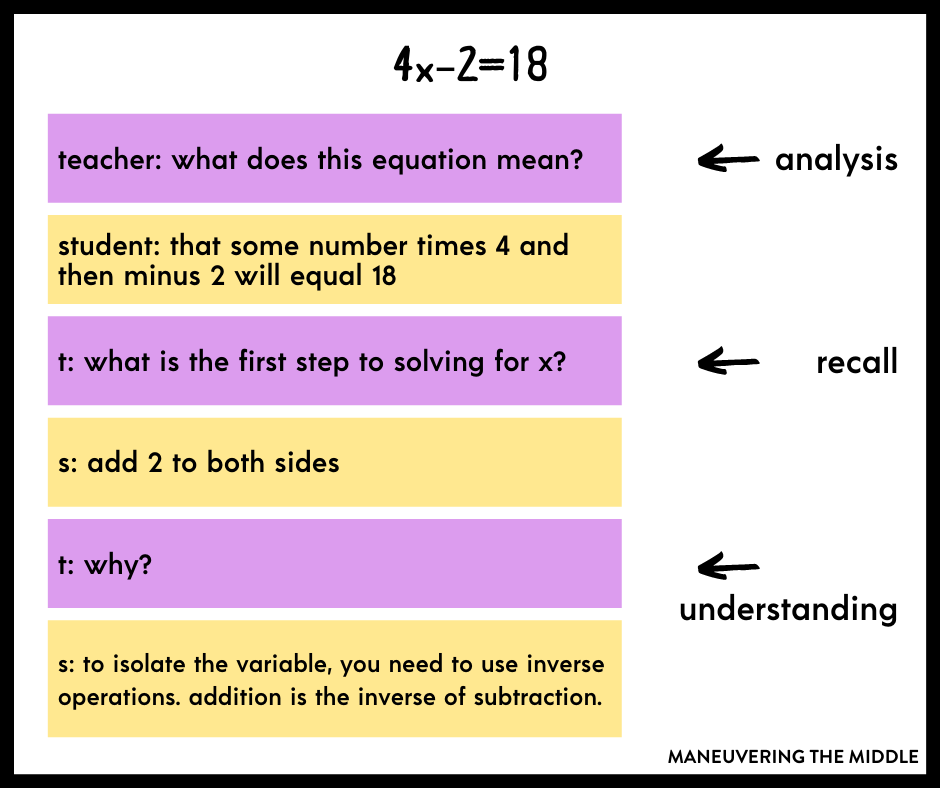
Let’s try a non-example in a typically procedural type of skill – solving equations.
Teacher: 4x-2=18 What do we need to do first?
Student: Add two to both sides. [Teacher adds 2 to both sides]
Teacher: 4x=20 And what do we do next?
And here is a way to teach the same problem using a mix of higher and lower order thinking skills.
This is where I would make a plug to use algebra tiles for this concept because students can visualize and explore how solving equations actually works with concrete models. When students move to the algorithm, their responses will be richer because the abstract is now concrete.
Not every skill or concept warrants a question in the highest order of Bloom’s Taxonomy. As you scaffold instruction, the types of questions you ask in Bloom’s hierarchy will move up.
You can find many question stems for math with a simple google search, so I took a problem from a He Said, She Said Activity from our Proportional Relationships bundle.

Wait Time & Eliciting Answers
In my fifth year of teaching, our campus read the book Quality Questions which helped me to learn about the technical term of “wait time” and that there were different wait times.
Wait time is the amount of time we sit in silence after a question has been posed. Then, there is actually a second wait timere which is the amount of time that you wait after a student responds.
The idea behind wait time is that we are giving time for students to think and that as soon as we accept an answer or acknowledge that the answer is correct, then everyone else stops thinking.
Here are a few ideas to incorporate this into your classroom:
- This can be that they have to write something down, show a finger for a multiple choice response, or they share their answer with a partner while you circulate.
- I like to give students a little bit of heads up if I want them to share, known as “warm calling”. You ask a question, give a minute of silent think time, ask students to share with their partner, and then circulate. I listen to things I want the whole class to hear. If I hear a great response from a student, I let them know that I would like for them to share, so they aren’t caught off guard. Then when we come back together as a class, I have that student respond.
- You can do a fist to five. Typically, fist to 5s are used at the end of the lesson for students to gauge how well they feel about the lesson on a scale from 0 (did not understand) to 5 (completely understand). In the case of answering a question, you can require all students to show their fist to five to assess how well they think they can answer the question. It actually gives you some information – which students are completely lost, which students are ok, and which students think they have exemplary responses. I would call on a mixture of 4 and 5s while making sure my fist and 1 students are listening in. Then I will go back to a fist or 1 student and ask for them to put the response in their own words.
Note: I didn’t do this for every single question I asked. Who has the time? I reserved these techniques 2-3 times a lesson for questions that warranted more time and thought.
Two Quick Hits
This first idea comes straight from Building Thinking Classrooms. Before you model a skill, first give students the problem and ask for them to try it on their own. Give them just enough background knowledge to get them started.

You can do this for many math skills. Estimating square roots, operations with rational numbers, geometry skills, solving equations. It doesn’t have to be done daily, and use your discretion for when this approach may not benefit students.
My second quick hit is something that I picked up in a training that made a huge difference in how I ended my lessons. I adjusted my language from, “Are there any questions?” to “What questions might someone have about what we learned today?”
- The former resulted in silence. And made me think as a teacher that I was good to go.
- The latter resulted in students trying to think of something that wasn’t covered. In addition, students who may not want to admit that they have a question or don’t understand something, would be more willing to inquire.

How do you incorporate higher level thinking in your teaching?