The CRA framework is an instructional strategy that stands for concrete, representational, and abstract; it is critical to helping students move through their learning of math concepts. 

To fully understand the idea behind CRA, or concrete representational abstract, think about a small child learning to count. They may learn counting to 10 by memorizing a song. Then, these numbers are used to teach them to count. First, they may be counting blocks by pointing or moving the object. Then, they may be able to count dots on a page or something on paper that represents that same concept. Lastly, they may be able to then look at a picture with five dots and not need to count it, they have learned what five “looks like”. This process takes place with all different math concepts and new learning.

Looking for more math intervention ideas?

This is part 3 of our Instructional Design series. We’ve covered how to unpack math standards and how to use questions to push students to think more critically. Make sure to grab our lesson planning freebie down below!

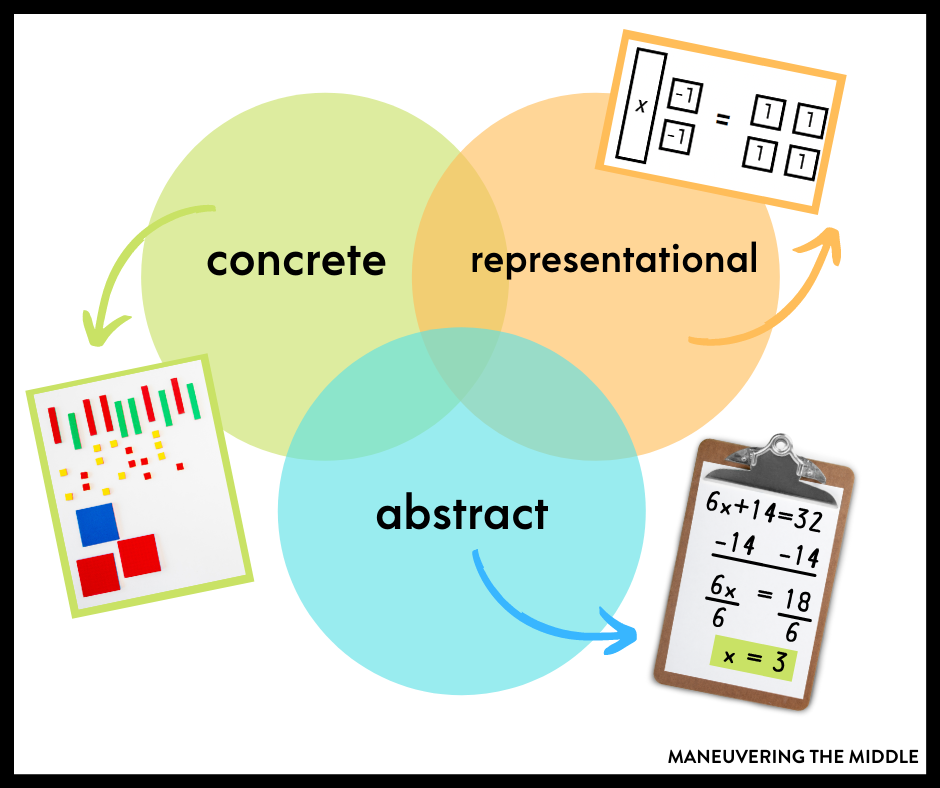
What is the concrete representational abstract framework?

The CRA framework helps us to present this learning in a specific method to help tie all the connections together. There have been numerous studies measuring the effect of using the concrete representational abstract (CRA) sequence for students at risk of failure. You can read more here, here, and here. 

This teaching method breaks down the concept (examples: multiplication, subtraction with regrouping, subtracting integers) in a methodical process in which students move from one phase to the next.  

Sometimes CRA is referenced as a sequence, so moving from one phase of understanding to the next. But more so, it is called a framework, which shows that all three of the representations can be used simultaneously. If we were teaching solving equations, students would actually use the algebra tiles, draw a picture of the model, and then write it mathematically at the same time.

Concrete

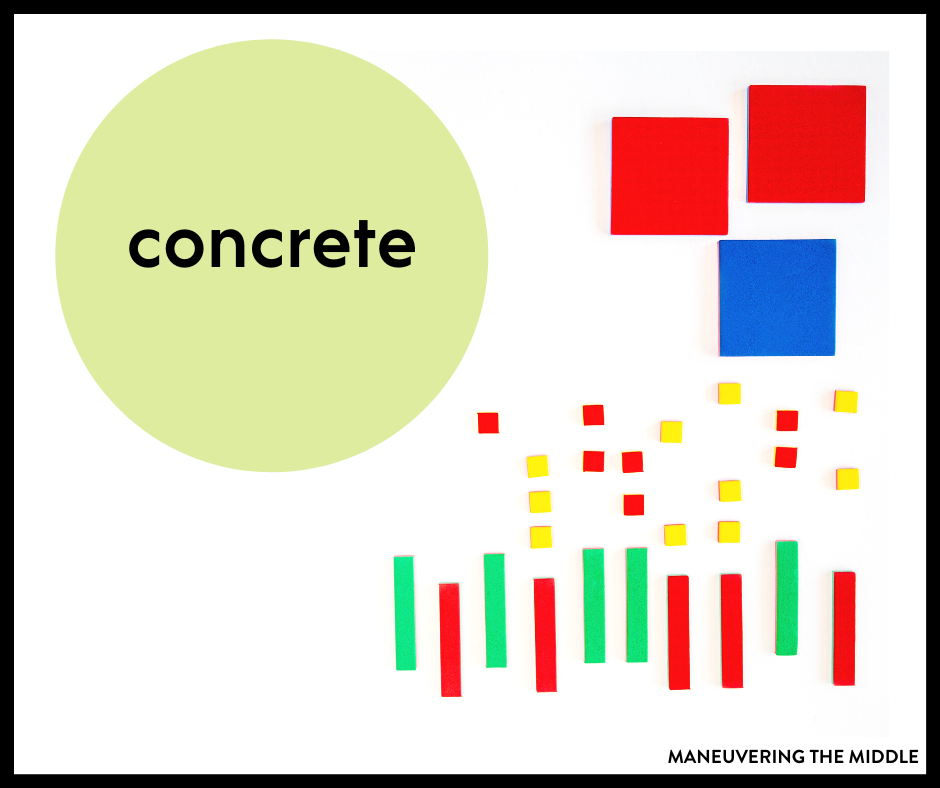
When students have a concrete understanding of a mathematical concept, they are utilizing manipulatives to demonstrate the math.  For example, when my son was learning to count, I wanted him to physically touch or move the items he was counting. In doing this, he was developing one-to-one correspondence.  He was internalizing that each item represents one.

When our middle school students are learning to solve equations, we want them using algebra tiles to physically remove manipulatives from both sides of the equation.  This allows students to internalize that an equation must remain balanced.

There are many reasons why teachers might skip this crucial step:

• Practice with concrete manipulatives takes time and energy. It is not easy to facilitate with 30+ students.  
• It can be expensive to purchase manipulatives.
• It can be frustrating for students who seem to already grasp the concept.  

Why it is beneficial:

• Students are using their kinesthetic learning style.
• Students are engaging with the content in a deeper way, and abstract concepts like “isolating the variable” are given meaning.
• This foundation is formidable so that they can move to conceptual understanding and aren’t just following a list of steps with no meaning.
• Research shows that it is essential for students who have a shaky math foundation.

Representational

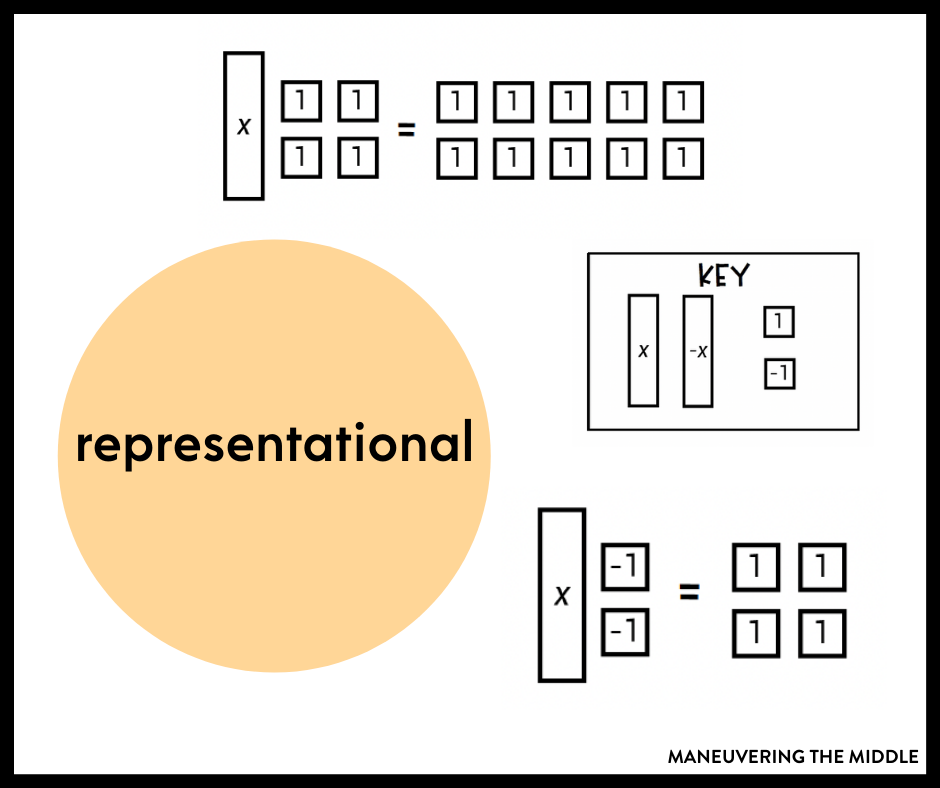
The representational part of the framework refers to students drawing a representation of those concrete materials. 

In the case of my son above, that would be counting dots on a page or drawing eight tally marks to represent the number 8.  

In the case of our middle schoolers and solving equations, this would look like drawing the algebra tiles, creating a key, and demonstrating how the process works by crossing off the tiles or grouping as they solve.  

We see this quite a bit in middle school.  From integer counters being sketched to a graph that represents a linear relationship, our standards include many representational aspects. 

Why We Might Start Here:

• This is a little easier to execute in a classroom full of students.
• The standards include the representational language. 
• It also leaves some gaps for students who need to understand why you are crossing out the positive integer circles.

Abstract

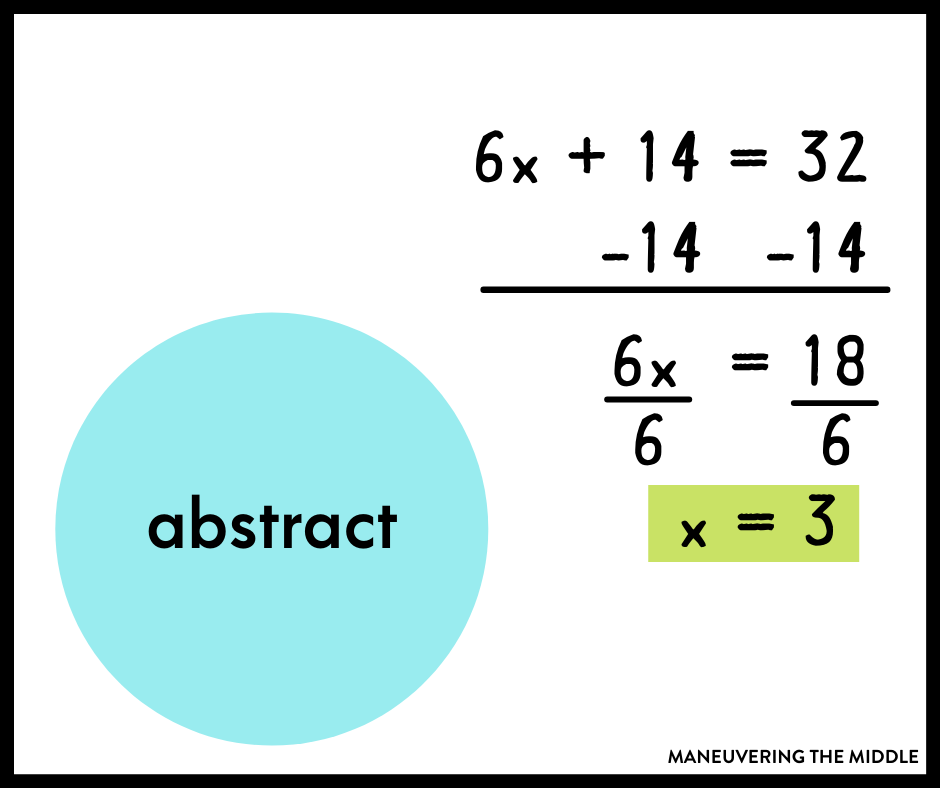
Math can be a very abstract subject.  When you think about solving an equation and finding the value of x, why are we doing this?  Why do we need to know this? The value of x is abstract. It is always changing. It doesn’t actually mean anything without context.

I think this is where it is really difficult for students who struggle.  When we don’t provide a context for learning and for the application of the abstract, it just seems too confusing.  I think it also warrants the phrase, “I don’t get it.” Many times students don’t even know what to ask because the content means nothing to them.

This is when math becomes too procedural and you risk students understanding the process, going through the motions, and yet lacking number sense.  When I was a student, I was taught solely in the abstract. It wasn’t until I was a teacher trying to make sense of models before I had several AHA! moments. Why didn’t I learn this when I was in school??

Best Practices

Shelley Grey says, “When you teach a math lesson, make it your goal to incorporate concrete, representational and abstract into the same lesson. This way you can be certain that you are differentiating for all your students, regardless of where they are in their understanding.

And it does naturally lend to differentiation — you are scaffolding, using different parts of the brain, and then eventually allowing students to work with a method they feel comfortable with. 

You as the teacher can make sure to use different methods when you are tackling problems. Just because you taught the algorithm for multiplying fractions already doesn’t mean you can’t draw a model to solve at a later date. This ensures that students don’t forget how to use the models themselves.

How do you teach difficult math concepts?