Unpacking Math Standards When Lesson Planning

Unpacking math standards helps teachers build the foundation for what content they are teaching to students. Subsequently, unpacking math standards provides a framework to create actionable lessons. Essentially, unpacking math standards helps us answer these two questions:

1. What are students learning?
2. How will they learn it?

This is part 1 of our Instructional Design series. Come back to read more about higher level thinking and the CRA framework. And make sure to grab our free lesson planning template down below!

LISTEN ON: APPLE PODCAST | SPOTIFY

WHY DO WE LESSON PLAN?

Much like creating a to-do list to alleviate the mental load of upcoming deadlines, lesson planning keeps all of our thinking about a topic or skill in one place where it can be shared, referenced, and revised. 

When we are prepared intellectually to deliver a lesson, we allow for real-time adjustments and instruction to the depth the standards require. In addition, the physical plan allows a space for collaboration and feedback.

Not ready to lesson plan quite yet? Need the bigger picture?

Grab our FREE Middle School Math + Algebra 1 Pacing Guides.

MISCONCEPTIONS ABOUT MATH STANDARDS

• Standards do not need to be taught sequentially or in isolation. They do need to be organized with purpose though!
• Standards are not so rigid that there is only one way for them to be taught. 
• Standards are not to be interpreted in a vacuum. The more math teachers you can have in the process, the more likely you will have a full picture of the scope of the standard.

HOW TO UNPACK MATH STANDARDS

Let’s talk about how we go about unpacking math standards using a 6th grade TEKS standard. 

• 6.7D: generate equivalent expressions using the properties of operations: inverse, identity, commutative, associative, and distributive properties
• This comes from the strand 6.7 “The student applies mathematical process standards to develop concepts of expressions and equations”

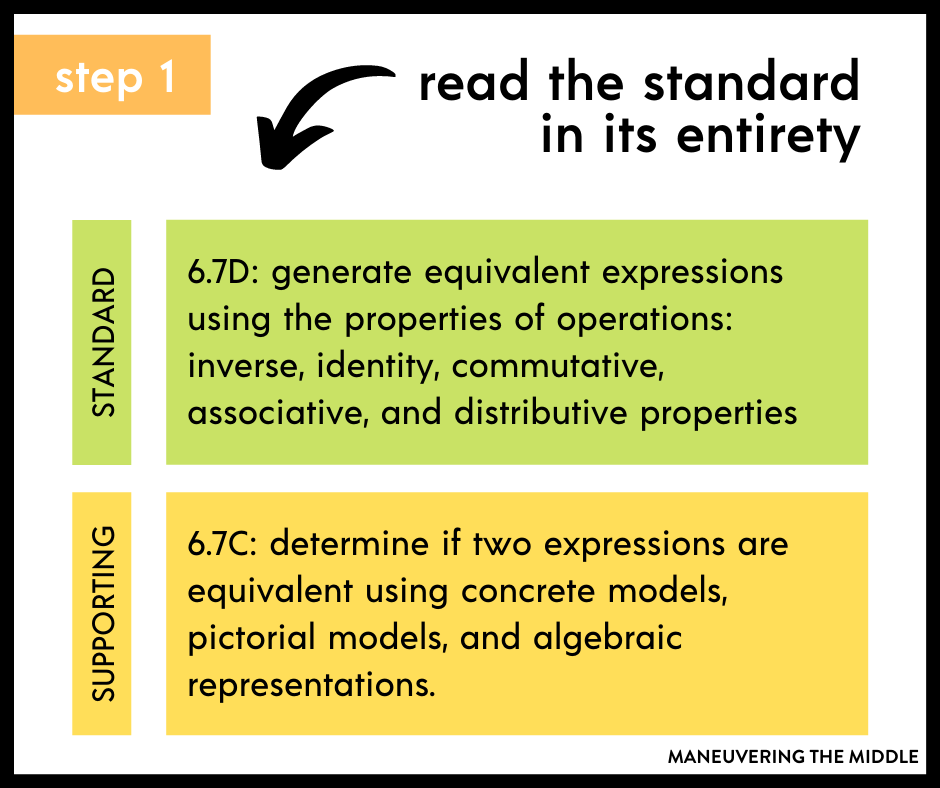
Step 1 – Read the standard (and related standards) in its entirety

• There is a related standard that asks students to determine if two expressions are equivalent using concrete models, pictorial models, and algebraic representations. (6.7C) 
• This is helpful because I can support my instruction of that initial standard with concrete and pictorial models. It gives me more information about how I can teach it.

Step 2 – Create a T chart listing the knows and the dos 

• The Dos are the verbs. What the student is expected to do.
• Examples include: apply, solve problems, represent, determine, calculate, predict, write, model, compare, convert, and describe. 
• Make sure that whatever the student is doing in class is the same as the verb in the standard or that the lesson will eventually support it.

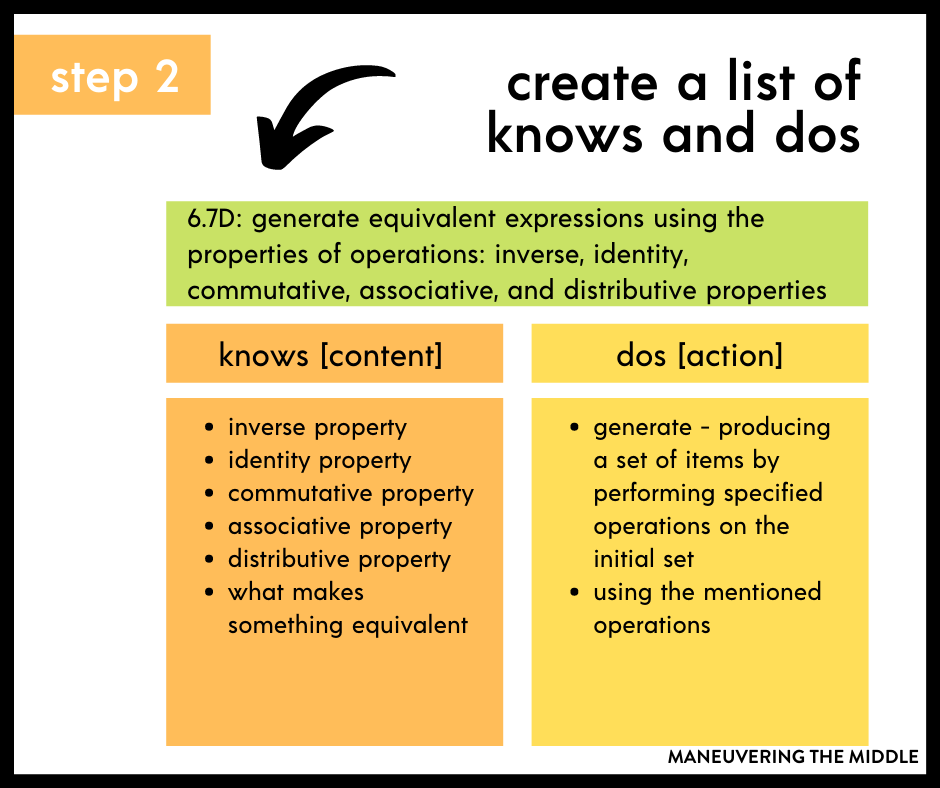
• It is crucial to understand what the verb means. Oxford dictionary defines generate (in the math context) as producing (a set or sequence of items) by performing specified mathematical or logical operations on an initial set. The lesson should be focused on the student creating equivalent forms of the expression using the properties.
• The Knows are the content. The knowledge that the student must have to execute the verb.  Typically, this is going to come from the nouns. So in our case, students will need to know how all of the properties function in order to generate equivalent expressions. 
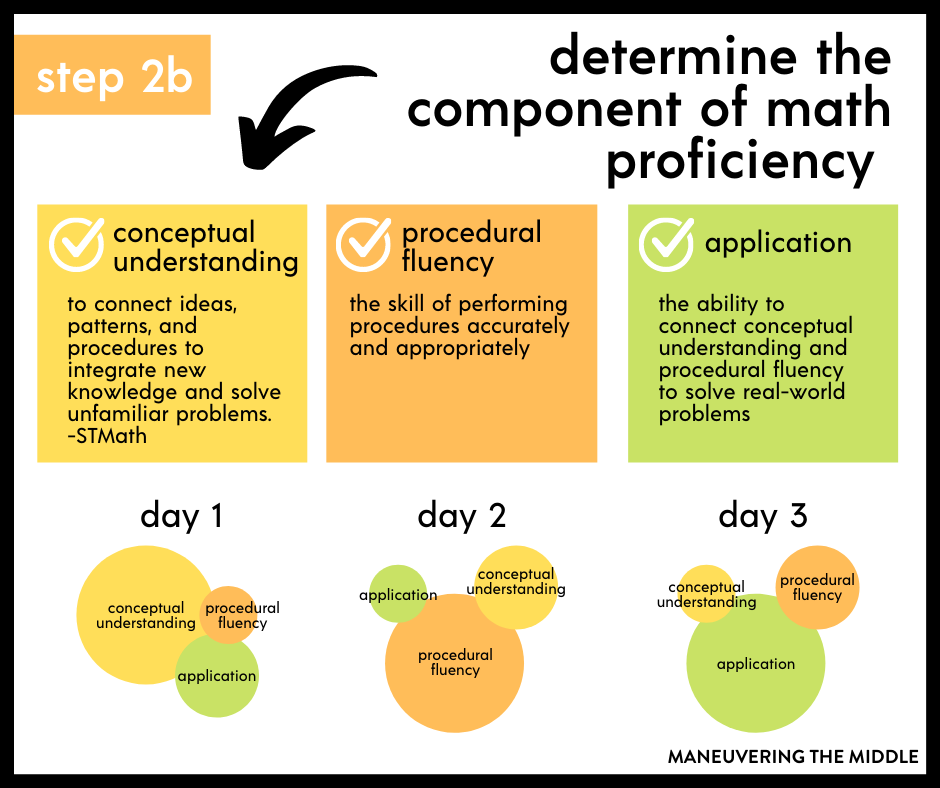
• One other best practice to unpacking math standards is to determine if the standard is more conceptual, procedural, or application. If the standard is very procedure heavy, I am going to want to make sure that there is some conceptual understanding introduced and application type of problems too. We want our lessons to be well rounded.
• If you have done this and are still unsure what the standard means, then I recommend looking at a state test question to see how the standard is assessed. 

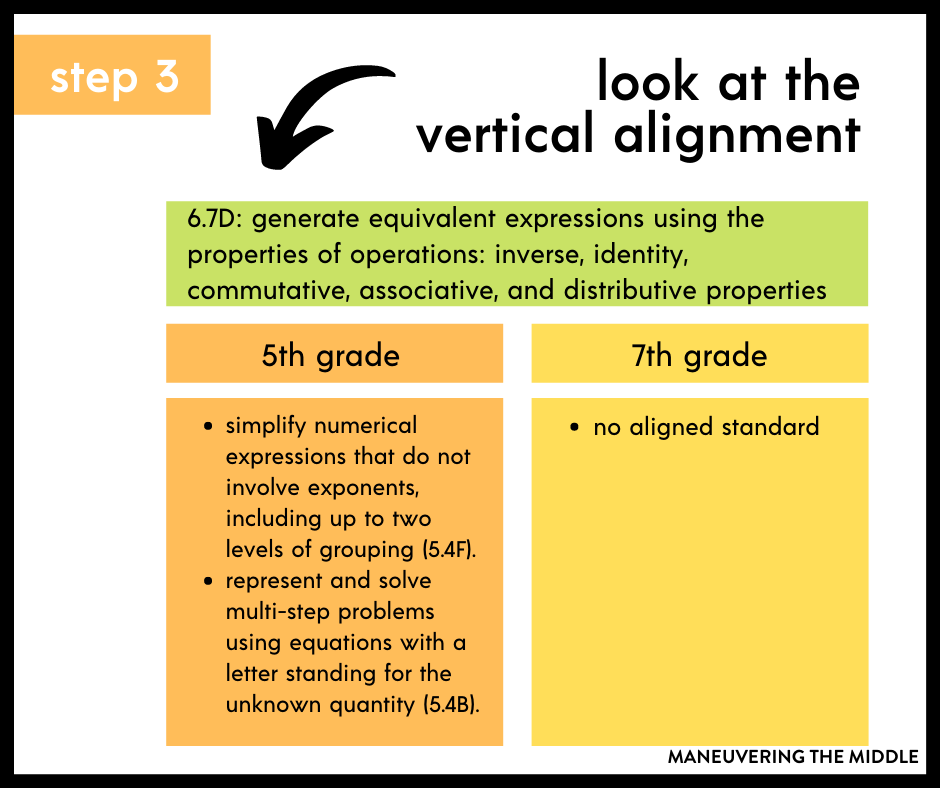
Step 3 – Look at the vertical alignment

Texas teachers, grab yours here. I like to read the math standards that are connected from the previous year to see what my students should know already or more likely, what I will need to refresh them on before they can be successful with the new standard. 

Step 4 – Write a learning target or lesson objective

Lesson objectives should be measurable and they should be student friendly. Different schools follow different guidelines – your school might use “I CAN statements” or “student will be able to” language. My preference is below:

Remember that whatever question, problem, or activity your students are completing, it should support your learning target or objective.

Step 5 – Write Big Ideas and Essential Questions

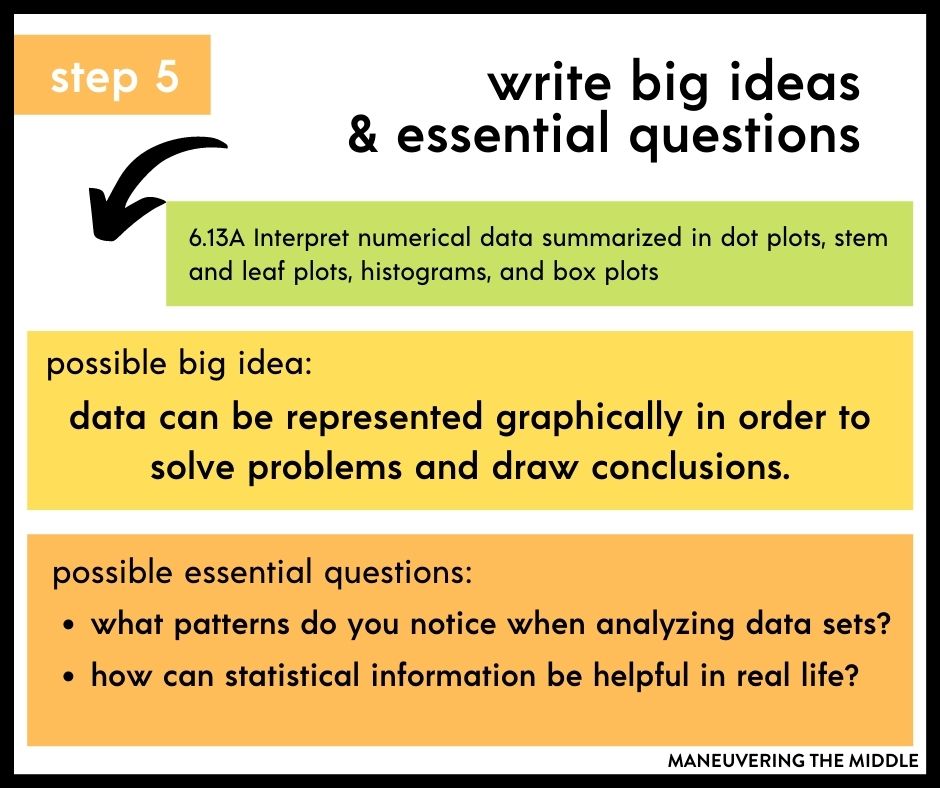
Big ideas are the concepts that transcend your unit and connect the content to their real lives and make it relevant. Perhaps students won’t walk away from your data and statistics unit remembering exactly how to find the median, but they will take the big idea that data can be represented graphically in order to solve problems and draw conclusions. 

Essential questions support your unit’s big ideas. These are recurring questions that can be asked all unit long that are designed for students to have that lightbulb moment. They allow open ended discussion from your students and to stretch the thinking of your students. Use them at the beginning of your unit to pique student interest and/or at the end of the unit to summarize or synthesize their learning over the last few weeks. 

How do you unpack math standards? What is your lesson planning process?