Factoring trinomials relies on many prerequisite skills (distributing, multiplying polynomials, finding a greatest common factor, exponent rules, and integer operations… I’m sure there are more). It also sets the stage for future success in solving quadratic equations and graphing quadratic functions.
This makes factoring polynomials so important for students to conquer. As a student, I remember only learning to guess and check, and lucky for us now, there are better ways!
Introducing Factoring with Algebra Tiles
I learned this method from Making Math Moments. You can watch the full video here or read on. Before even introducing factoring polynomials, ask your students to represent a trinomial using Algebra tiles like this one below:
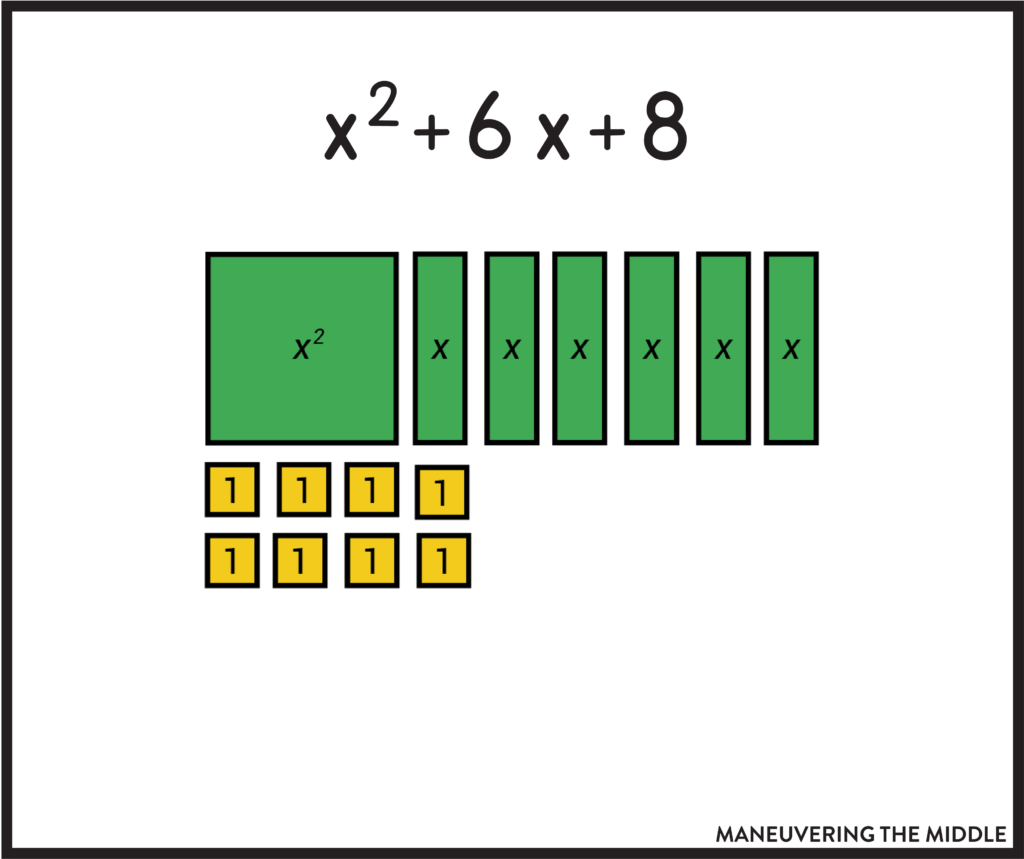
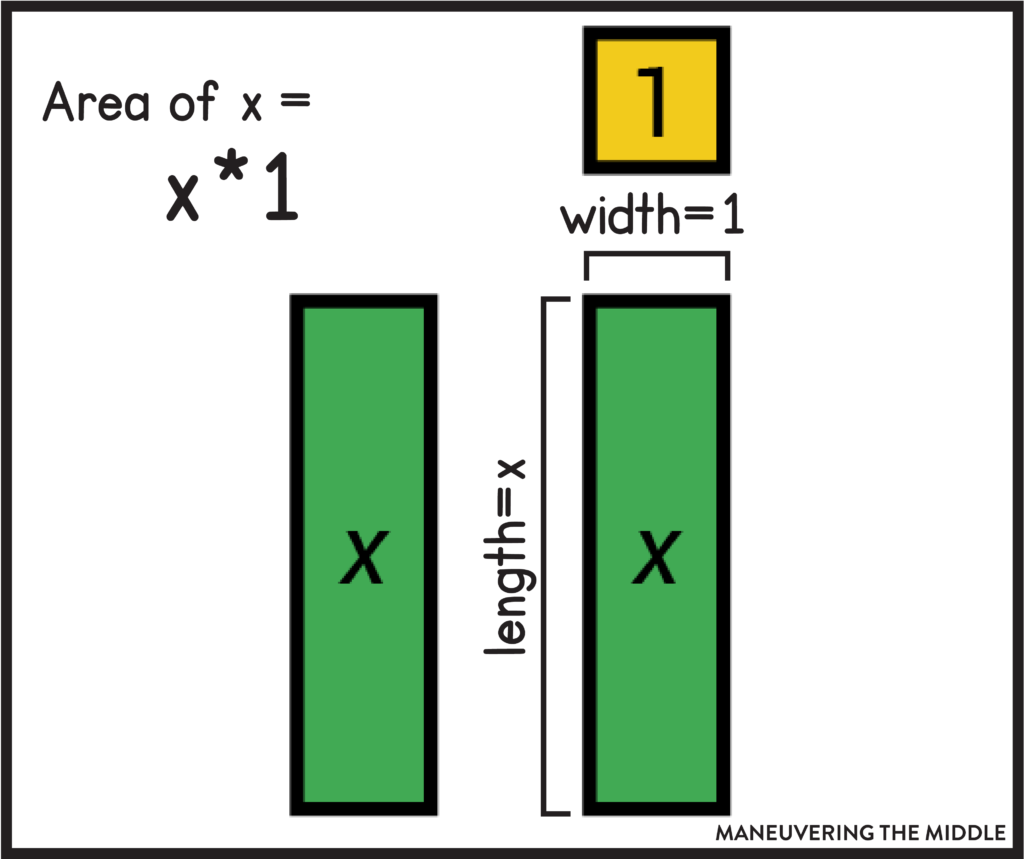
Before proceeding, make sure your students understand that the area of the x tile is x*1.
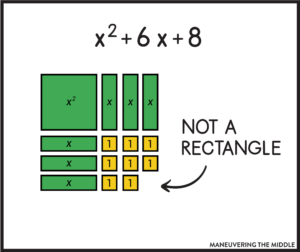
Then ask your students to arrange the tiles in a rectangle using all of the pieces. Let them solve this puzzle – they may leave pieces out or create a shape that isn’t a rectangle.
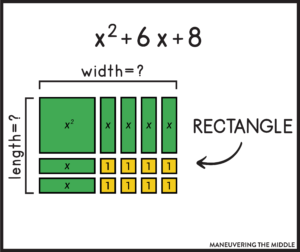
Then ask them to figure out what the dimensions (the length and the width) of the rectangle would be. You haven’t explicitly taught factoring at this point. You are letting students explore and come up with their own patterns using hands-on practice. Here is the solution:
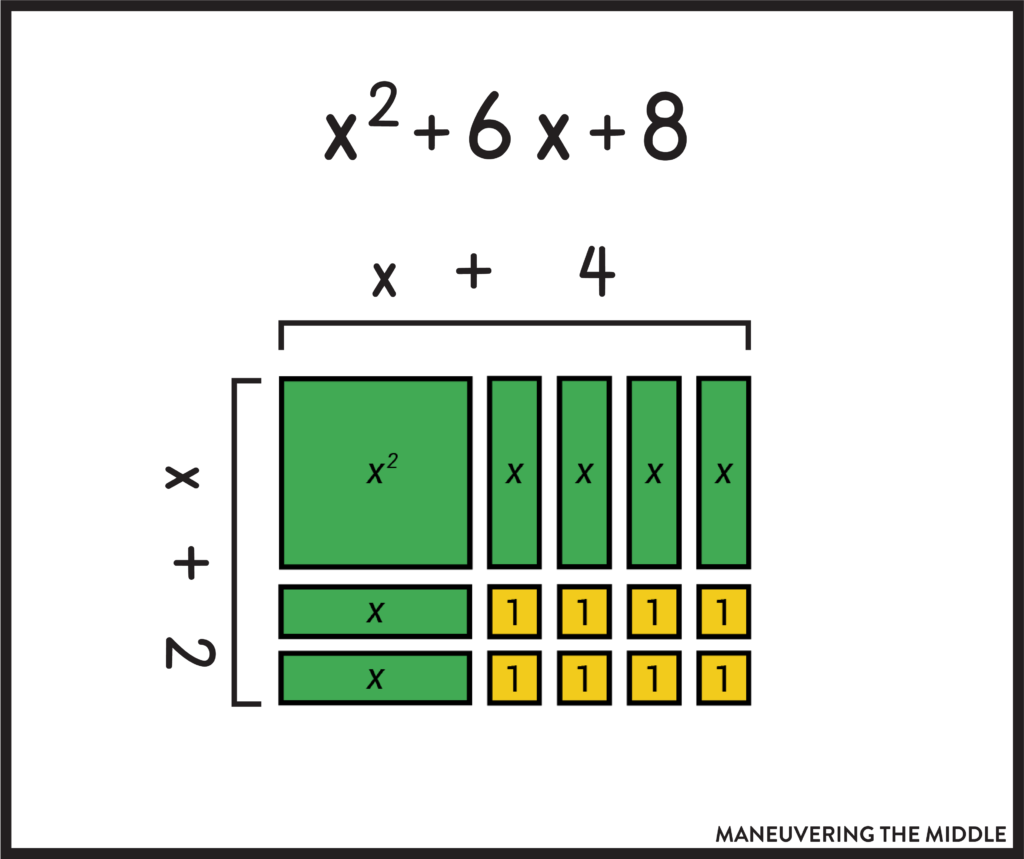
Maneuvering the Middle’s Factoring Polynomials Modeling Activity is the perfect way to introduce or practice this skill. You can find it in our Factoring Polynomials Activity Bundle.

Start with the Greatest Common Factor
Students won’t get far without mastering factoring out the GCF.
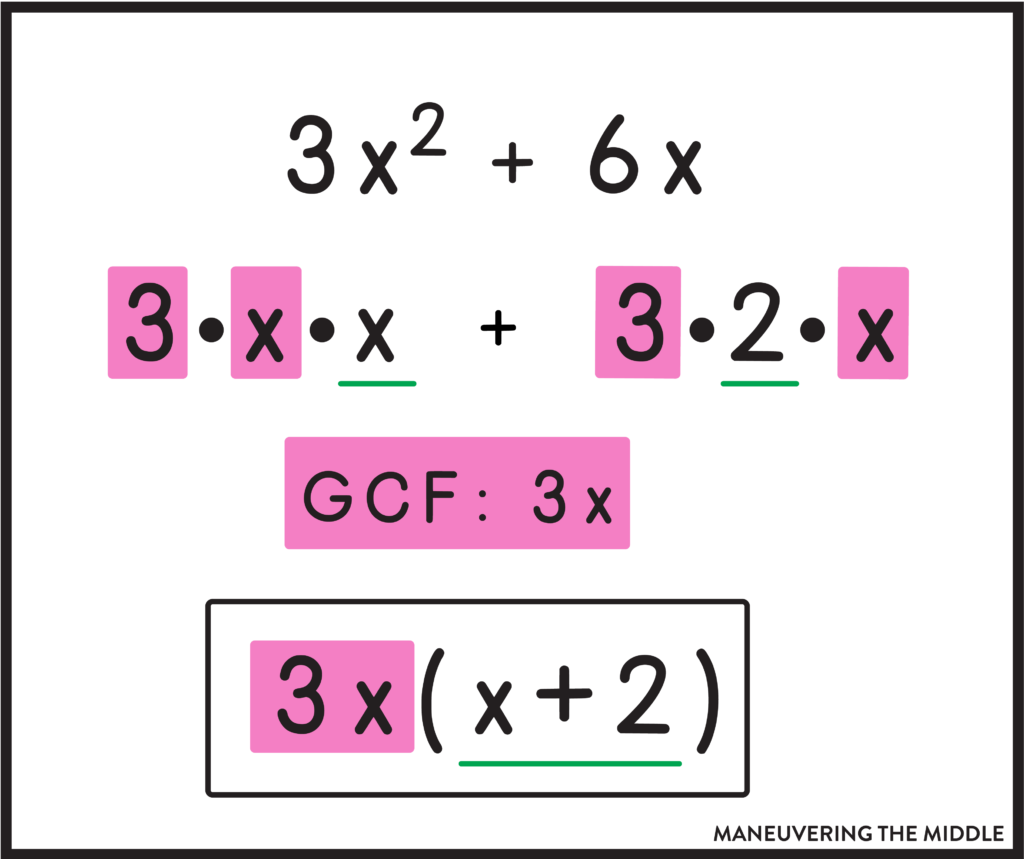
Start by teaching students to write all of the factors of each term and circle/highlight the factors that they each have in common. Then whichever factors are not in common, will be the terms that remain.
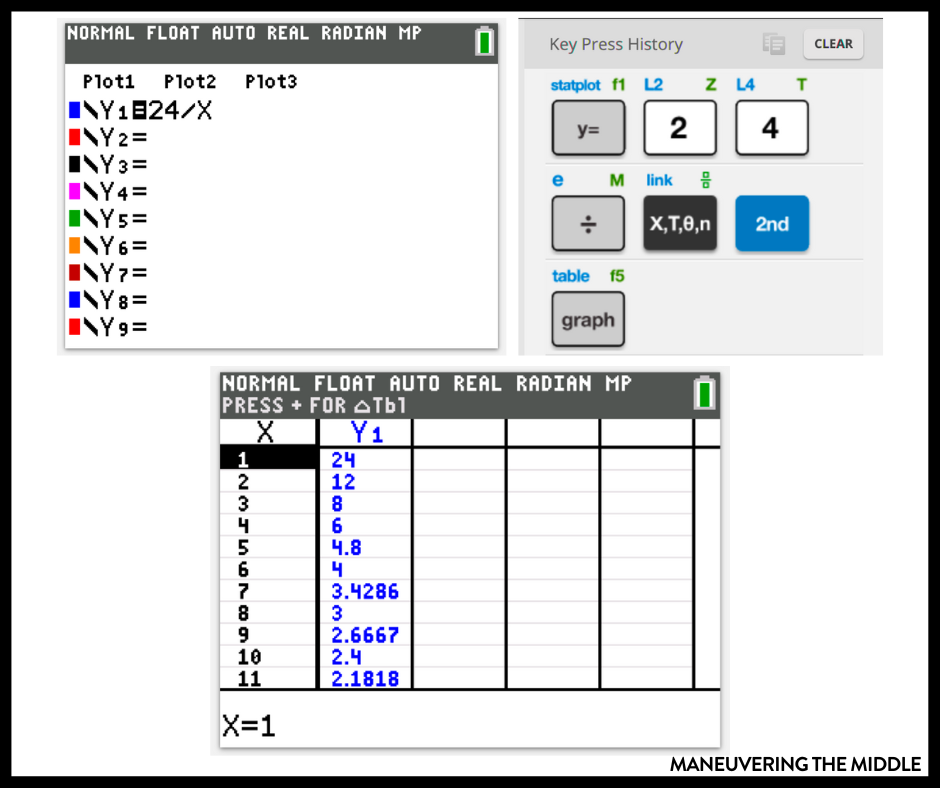
This idea is from our curriculum writer, Reagan. “When my kids struggled with factoring, it was usually because they didn’t have multiplication facts memorized. When students struggled with this, we taught them to use their calculator to type y = #/x and look at the table to easily see all the factors.”
Factoring Trinomials When A=1
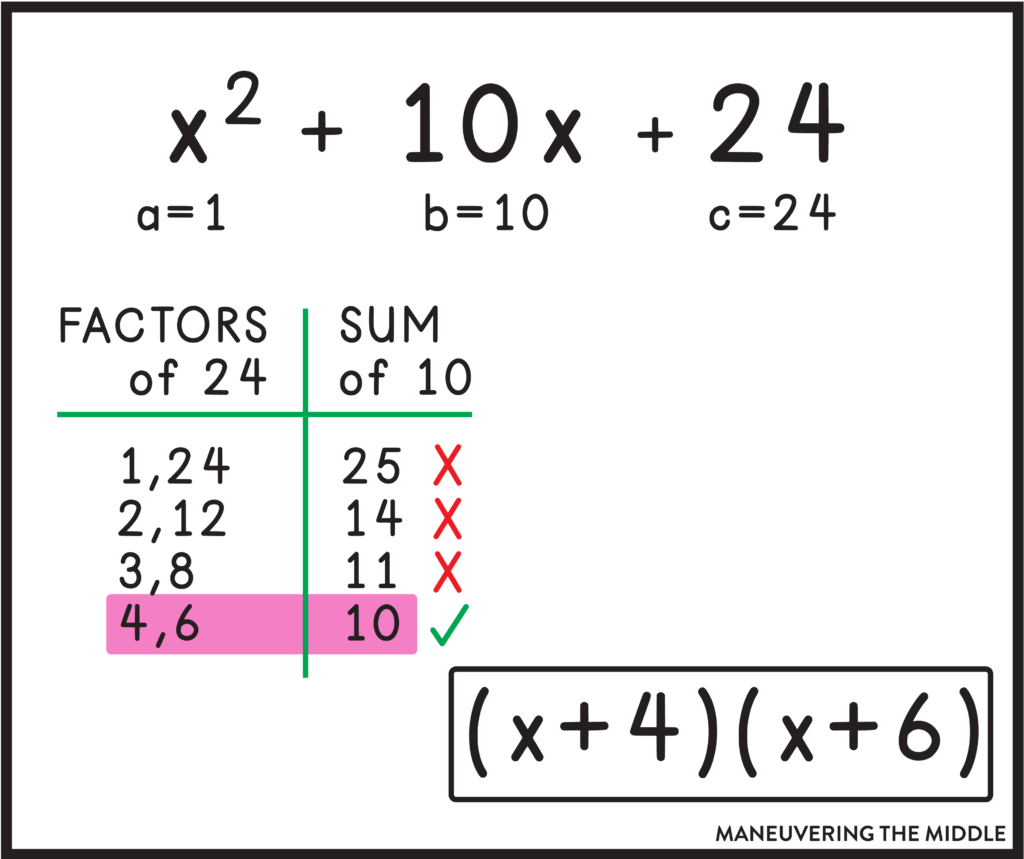
Keeping students’ work organized is key when teaching this skill, which is why I highly recommend showing students to organize their work using a sum and factors table. In the example above, you can see that the b term is the sum of 4 and 6 while simultaneously, the c term is the product of 4 and 6. Simply put, I would ask my students when trying to factor:
- What multiplies to c (24) that also adds up to b (10)?
If we couldn’t think of it off the top of our heads, we would make a table (which is especially helpful when you have a negative b or negative c term.)
Watch the video to see how Sara teaches this:
If you love this video, check out All Access for more student videos!
Using The Box Method
The box method is also a great tool to familiarize your students with factoring. The same thinking of “what are the factors of c that will also add to b?” is required, but your students will practice more with finding the GCF of two terms which will set them up nicely when a>1. This silent video explains how to do this quite well.
You can also follow the visuals here:
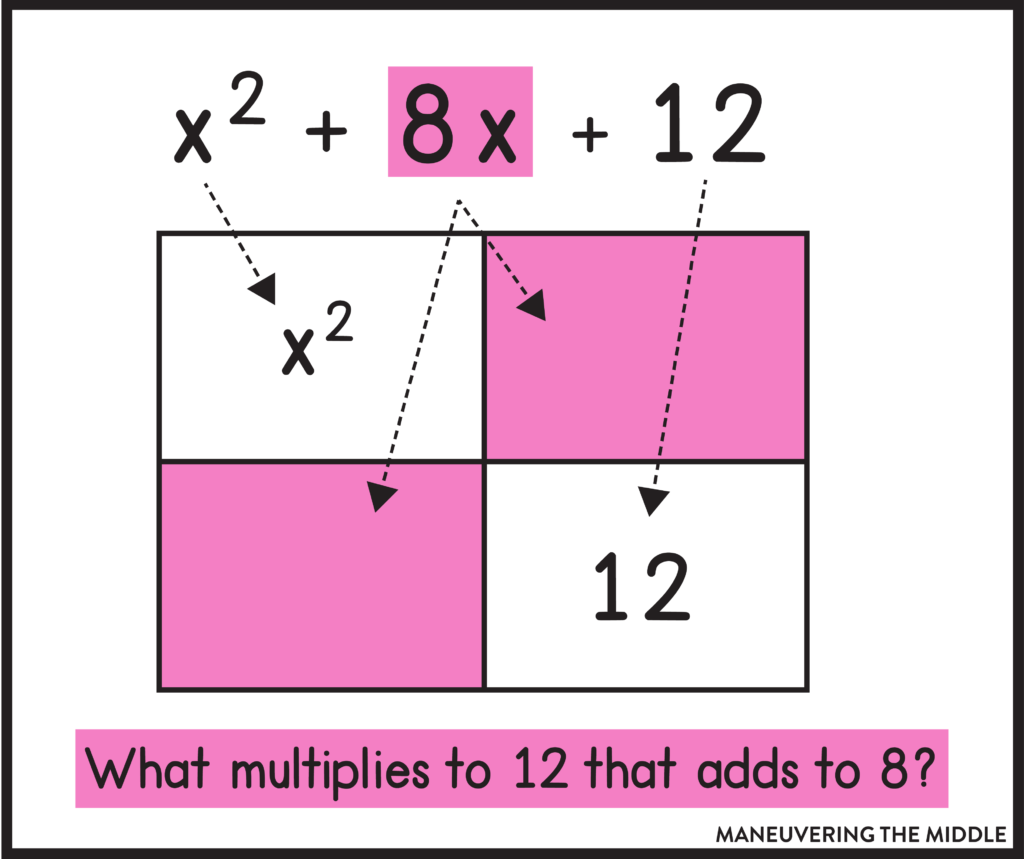

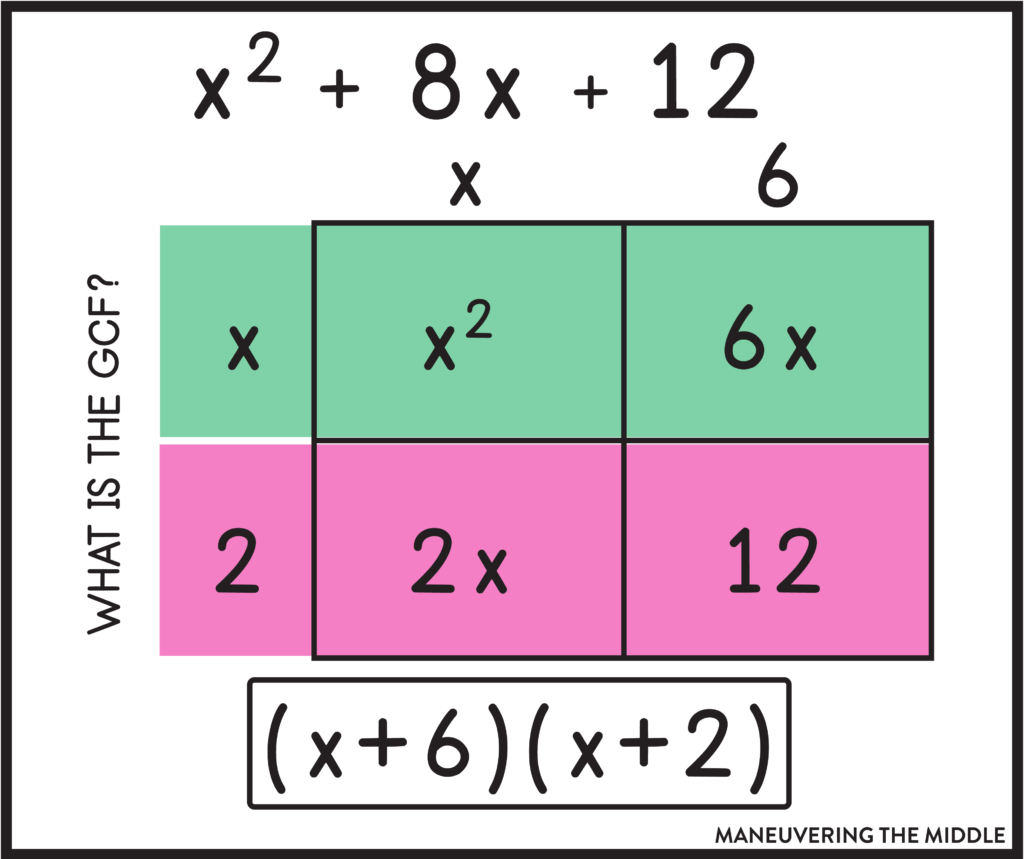

If you are looking for some additional resources to use with your students, then check out the links below:
- CCSS Factoring Polynomials Unit
- TEKS Factoring Polynomials Unit
- Factoring Polynomials GCF Digital Activity
- Factoring Polynomials a=1 Digital Activity
- Factoring Polynomials Activity Bundle
- Factoring Polynomials Digital Activity Bundle
Make sure to come back next week when we talk about Factoring When a>1 and Difference of Squares and Perfect Square Trinomials.
How do you teach factoring trinomials?





