Multiplying and dividing integers is the perfect math concept – the computation is relatively simple, there are opportunities for hands-on learning with manipulatives, and there are an abundance of explanations that support the conceptual understanding.
However, it is a little tricky! Be sure to read “How to Teach Integer Operations” where we cover the specifics on adding and subtracting integers, as well as some common misconceptions to avoid.
Multiplying and dividing integers is taught as early as 6th grade (in Texas) but primarily introduced in 7th grade. Multiplying and dividing integers extends into rational numbers which means there is a lot to cover!

Tip #1: Start By Using Models or Manipulatives
“Tricks” definitely have their time and place in math, but building conceptual understanding is key for students to build that mathematical fluency. Since math is always progressing and building on itself, tricks can often be mixed up with other tricks. Anyone who has taught integers or fraction operations probably has experienced this first hand. (Keep, change, flip or keep, change, change?)
Modeling why like signs result in a positive answer and why unlike signs result in a negative answer is more likely to stick than having students only copy down the “rules.” Though I do think it is helpful to do that too! In fact, I kept an anchor chart with all of the rules posted throughout most of the school year.
Here is a helpful Google Slide Deck that I recommend using to introduce WHY a positive times a negative results in a negative product and WHY a negative times a negative results in a positive product. I used a number line to introduce this concept, but counters can work too.
Here is the slide deck for you to copy and use in your classroom! The animations are included, so you just have to click your mouse to make the arrows move.

If you prefer counters, here is how I would teach positive times a negative.
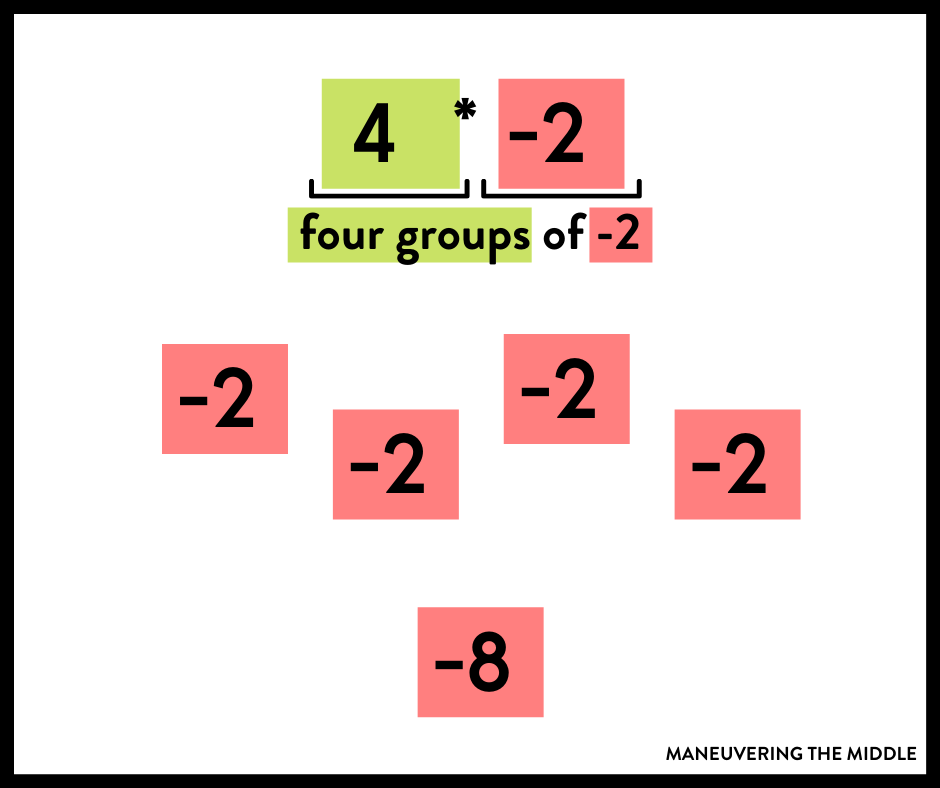
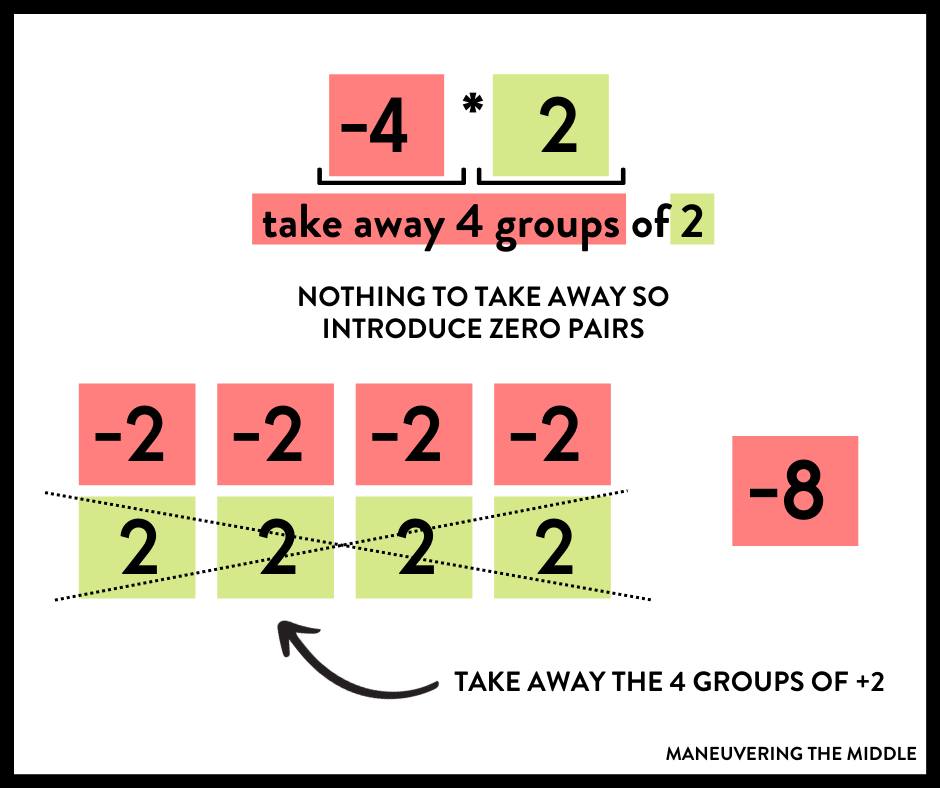
And a negative times a positive. One thing to note is since you can’t take away 4 groups of 2, you can introduce zero pairs. With the zero pairs, you now have 2s to “take away.”
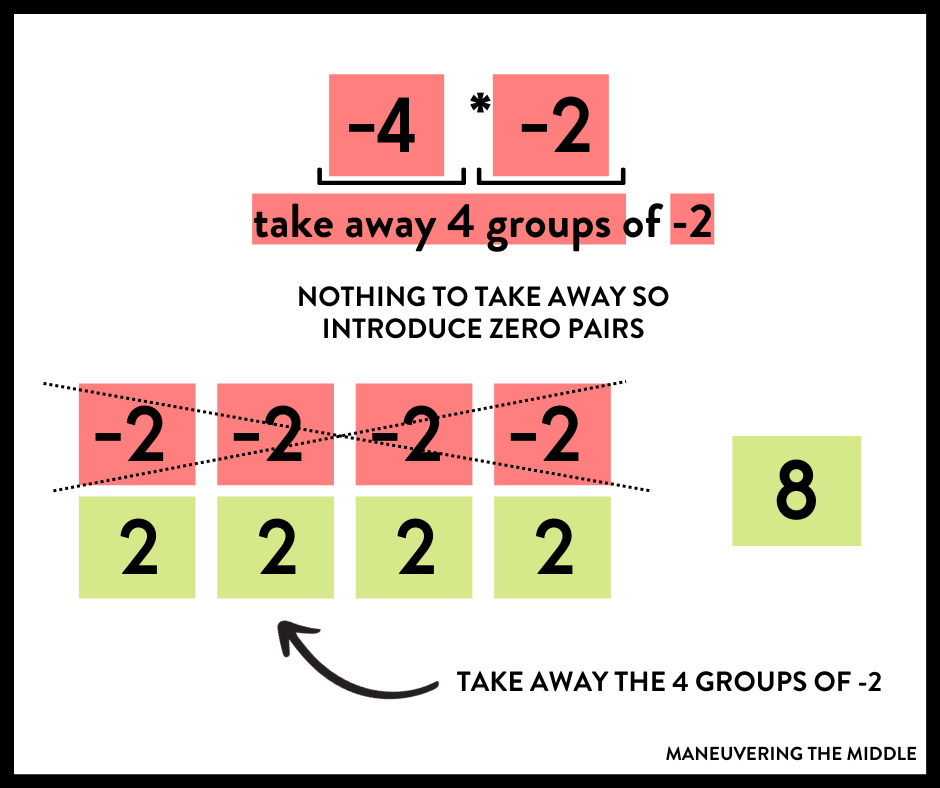
And lastly, a negative times a negative.
Tip #2: Ask them to Come Up With the Rules Using Patterns
The great thing about math is that the rules are always supported by patterns.
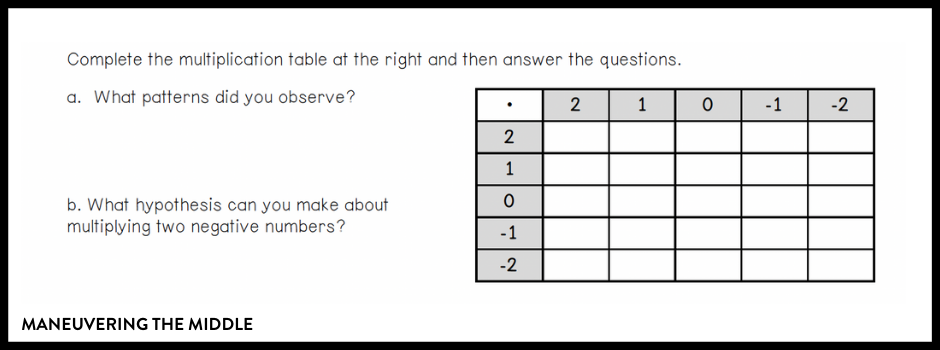
When using the above table (a snippet from a student handout), it is important to start in the top left corner where students are familiar with those facts. Allowing students to see the patterns that create the rules really makes the content stick.
You could give students a list of numbers like the one below and ask them to make observations about what they see. If a student can’t remember a rule, they can recreate a list of multiplication facts, and then synthesize the rules on their own.
- -5*(3)= -15
- -5*(2)= ?
- -5*(1)= -5
- -5*(0)= 0
- -5*(-1)= 5
- -5*(-2)= ?
- -5*(-3)= ?
Tip #3: Other Fun Ideas for Practice
- Give students a value they are trying to reach. Provide sticky notes or cards marked with a variety of integers. Students match integers to equal the given value. Similar to using counters, this allows for students to practice their fluency but also to be flexible problem solvers.
- Our MTM Activities – Entire bundle, speed dating, scavenger hunt and multiplying rational numbers digital activity, dividing rational numbers digital activity
- Playing War using this idea from Mrs. E Teaches Math.
- Make sure to include opportunities for real-world situations. Money, football gains and losses, temperature, and sea level are things that give these numbers context. Context provides students with opportunities for application as well as verifying if an answer makes sense.
- Make sure to buy and laminate these number lines. I would give my students dry erase markers to write on them.
Tip #4: Putting It All Together
In my experience, students are doing well and seem to really grasp when they are completing operations in isolation. Asking students to complete work where they are switching between the 4 operations or using them together can cause students to confuse what they have learned.
When that happens, ask students to draw a picture of what is happening. Send them back to the models because that is what they are there for – to make sense of the math. Don’t put the counters or number lines away just because you have already taught the models.
Since many students are resistant to draw models when they think they’ve “got it,” I would remind students that drawing the models accounted for half of the work/grade/completion. Once students mastered the four operations on a summative assignment, I would give them permission to use the algorithm only.
What tips do you have for teaching multiplying and dividing integers?




