Multiplying fractions: the good news – the process for teaching modeling fraction multiplication is much more straightforward than teaching dividing fractions with models! But if you are teaching fraction multiplication, then you will most likely be teaching dividing fractions shortly, so be sure to check out our dividing fractions post where you can get a free guide.
While the standards for middle school math do not include modeling specifically (those can be found in 4th and 5th grade), middle school students can benefit from growing their conceptual understanding.

Start with Whole Numbers
The basis of modeling fraction multiplication uses arrays. Before you jump into using arrays with fractions, start with modeling multiplication using whole numbers and arrays. Have students create their own arrays too.
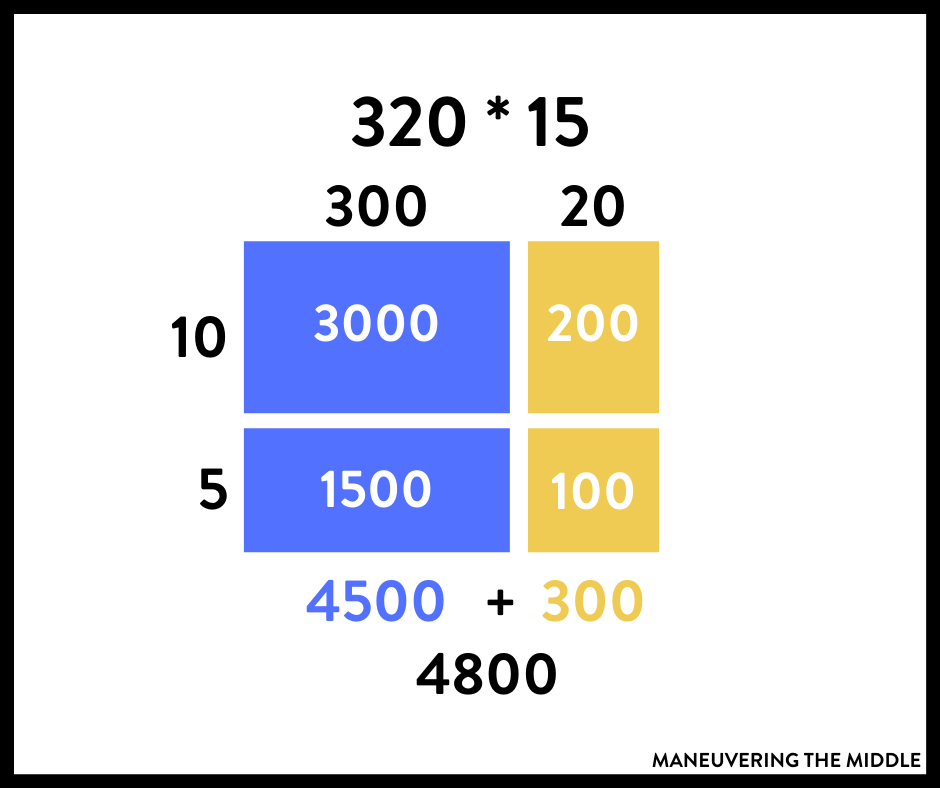
Anytime I am introducing a new concept, I connect it to something they already know how to do. This builds students’ confidence and creates more buy-in which means my job as teacher is a lot more enjoyable 🙂
Build the Conceptual Understanding Using Reasonableness
Before introducing the models, I want students to continue to build their reasonableness. Start with something that students are very familiar with like pizza.
Asking questions like –
- “If I have 1 pizza, and I eat ½ of it, did I eat more or less than 1 pizza?”
- “If I have 3 pizzas, and I burned ⅔ of them, how many pizzas did I burn?”
- “If I have 1½ of a pizza left and you ate ½ of that half, did you eat more or less than 1 pizza?”
One of the 6th grade TEKS standards is developing the understanding that multiplying a whole number by a fraction less than 1 will result in a product less than the original whole number, and multiplying by a fraction greater than 1 will result in a product greater than the original whole number. Using reasonableness can help support this standard and a conceptual understanding of multiplying fractions.
Modeling a Whole Number by a Fraction
4 times ⅖ can be interpreted as 4 groups of ⅖ or ⅖ + ⅖+ ⅖+ ⅖. This is the easiest to model. Draw a picture or use pattern blocks to demonstrate this concept for students.
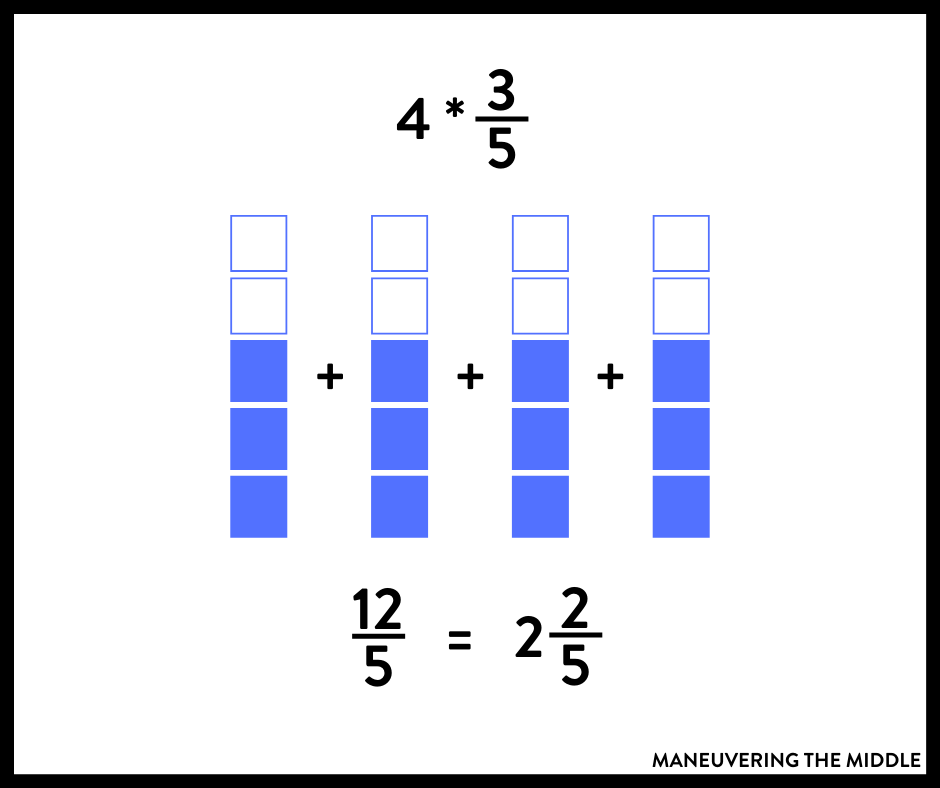
It gets a little trickier when you have ⅖ of 4. Sure you will get the same answer, but students do need to understanding that this means taking a ⅖ part of 4 wholes. If you haven’t checked out Mix and Math yet, Brittany is the queen of hand-on teaching in upper elementary math. Check out this video to see how she uses pattern blocks to teach these concepts.
Modeling a Fraction by a Fraction
If you need a refresher (or didn’t learn it this way yourself) this video explains how to multiply a fraction by a fraction using models. Again, this array will be more effective if you have introduced arrays with whole numbers first.
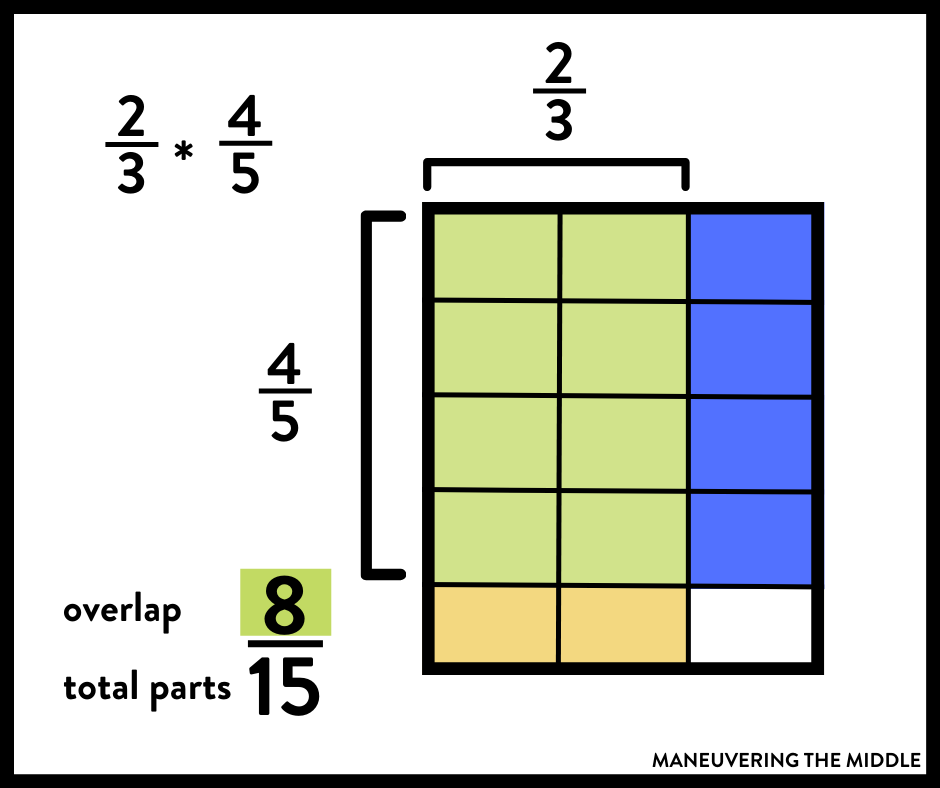
- Brownie pans or rice krispie pans are my go-to representations of this skill.
- Fraction Multipliers are manipulatives that support this skill. These manipulatives are very effective in a small group or intervention classroom.
Modeling Multiplying Mixed Numbers
In the past, I have taught students to convert mixed numbers into improper fractions and then to use the algorithm. This totally works! However, there are so many steps and so many places to make mistakes.
Here are a few tips to make this more manageable. Try using an area model to keep students’ work more organized.
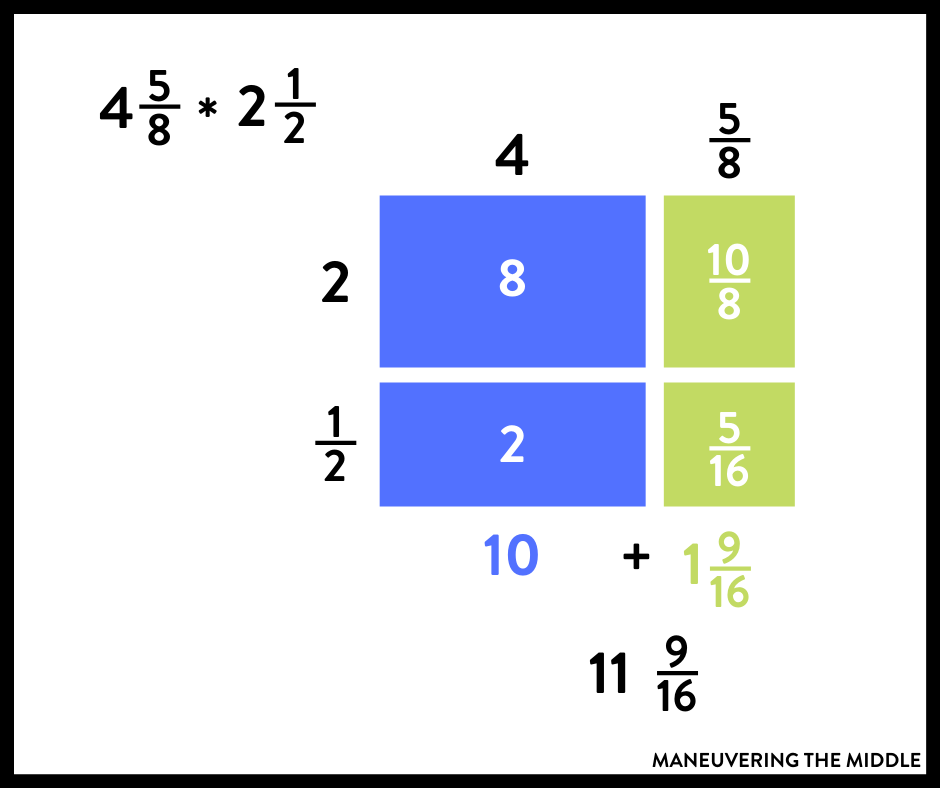
You can always have students make the problem simpler in order to estimate.
Let’s say the problem is 3 ⅜ times 5 ⅚. You could think of it as 3 ½ times 6. This becomes 3 times 6 plus 1/2 times 6. (Think: 34*5 is the same thing as 30 times 5 plus 4 times 5.) Therefore, 18 + 3 = 21. The answer to 3 ⅜ times 5 ⅚ is going to be verrrryyy close to 21. And since we rounded each factor up, I know my answer should be less than 21.
At the very least, you could have your students multiply the whole numbers to check that their answers are reasonable.
Additional Tips
- Give students the models and ask them to come up with the the number sentence that best represents it
- Remember that modeling isn’t just an introductory step. If you only use them to introduce the concept and never revisit, neither will your students.
- There is nothing wrong with the algorithm! Teach it, use it, and model it!
How do you teach multiplying fractions?




Hi
sorry mistake above
4 times two fifths