Are you eager for students in your classroom to conceptually understand integers and master the skills required for integer operations?
Keep reading and get individual sized and classroom sized vertical number line.

STUDENT Background WITH INTEGERS
If you are in a state that teaches Common Core, 6th grade is when the conceptual understanding of integers begins. Students are expected to be able to place and order integers on a number line, as well as determine opposites (6.NS.C.6.C). In Texas, students will be expected to do that and solve addition, subtraction, multiplication, and division problems with integers (6.3D). Mastering rational number addition, subtraction, multiplication, and division is required by the end of 7th grade in most states (7.NS.A.1).
Students’ previous knowledge includes operations for positive whole numbers and positive rational numbers. If you are a little unfamiliar with this vocabulary, then I included a diagram to help. And you can real more about how to teach the real number system here.
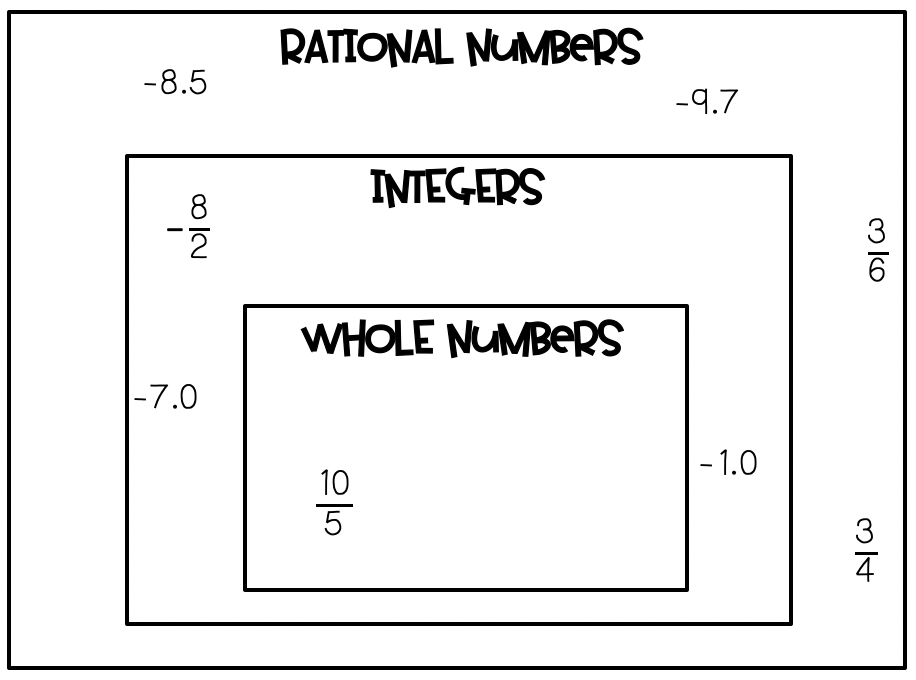
Students will not be asked to just solve these integers problems in isolation. They will be required to solve integer problems that include multiple steps, in order of operations problems, in solving for variables, and graphing.
Why are integers such a struggle?
Integers can be so deceiving. Students often think they are rocking it (it’s simple math, after all) only to be making the same mistakes over and over again. Unfortunately, as teachers, we can often say or do things that are actually detrimental to our students’ understanding of integers. For example, math students have heard from a young age that, “You cannot take a larger number from a smaller number” when, in fact, you can!
My weakness was my scope and sequence. I had one day to teach models, so I would cram the models for all of the operations into one or two days, and then make students practice using the algorithm over and over again. Each year, I spent more time investing students into the models, and each year, I saw my students’ confidence in working with integers improve.
No shame if you have taught tricks over conceptual understanding; I have! They are well intended. The tic-tac-toe to help with multiplication and division rules was taught to me! The problem with these tricks and shortcuts is that 100% of students will forget the trick or mix up the tricks with something else. If you have ever heard a student say, “Keep, change, flip” in response to how to solve an integer subtraction problem, then you know what I mean!
Ideas for Supporting Conceptual Understanding
Provide Context
While the term “integers” and the concept of using operations to solve integer problems are new to students, the idea of an integer is not new. Before jumping into integer operations, provide real-world examples of integers. Students are likely familiar with the following real-life scenarios:
- Owing and depositing money
- Losing and gaining yards in football
- A temperature below zero
- Above and below sea level
VERTICAL NUMBER LINES
If you don’t use vertical number lines, I would highly recommend you start using them! They give more context to above and below zero. Most real-world examples are more vertically inclined: a thermometer and above and below sea level. (I use a border to clean up my not so beautiful edges.)

Side note: Before jumping into showing students integer addition and subtraction using number lines, show students examples of addition and subtraction problems with positive whole numbers using number lines. I learned that some students had not been exposed to number lines for any operations. By modeling a few familiar problems, you avoid trying to teach two new skills at the same time.
Geogebra is a great tool to show addition and subtraction with vertical number lines. It’s interactive, so you could have students play with the website before introducing models or the algorithm. You could ask students what patterns they see and to derive some of the integer rules.
Subtracting integers has always been my Achilles’ heel. I had used “keep, change, change” to little success, but it wasn’t until I used the hot air balloon example that I saw students completely grasp why subtracting a negative would cause the answer to increase. Dropping sandbags off a hot air balloon would result in the hot air balloon moving up! (I made a very short video to demonstrate it)
Download, print, and cut out vertical number lines for your students here.
Counters to Show Multiple Representations
Another way for students to gain more of a conceptual understanding of integers is using counters to show multiple representations of a number.
For example, using counters, ask students to show -4. They might grab four red counters. Ask them to show -4 another way, and they might not know what to do, or they might say there isn’t another way.
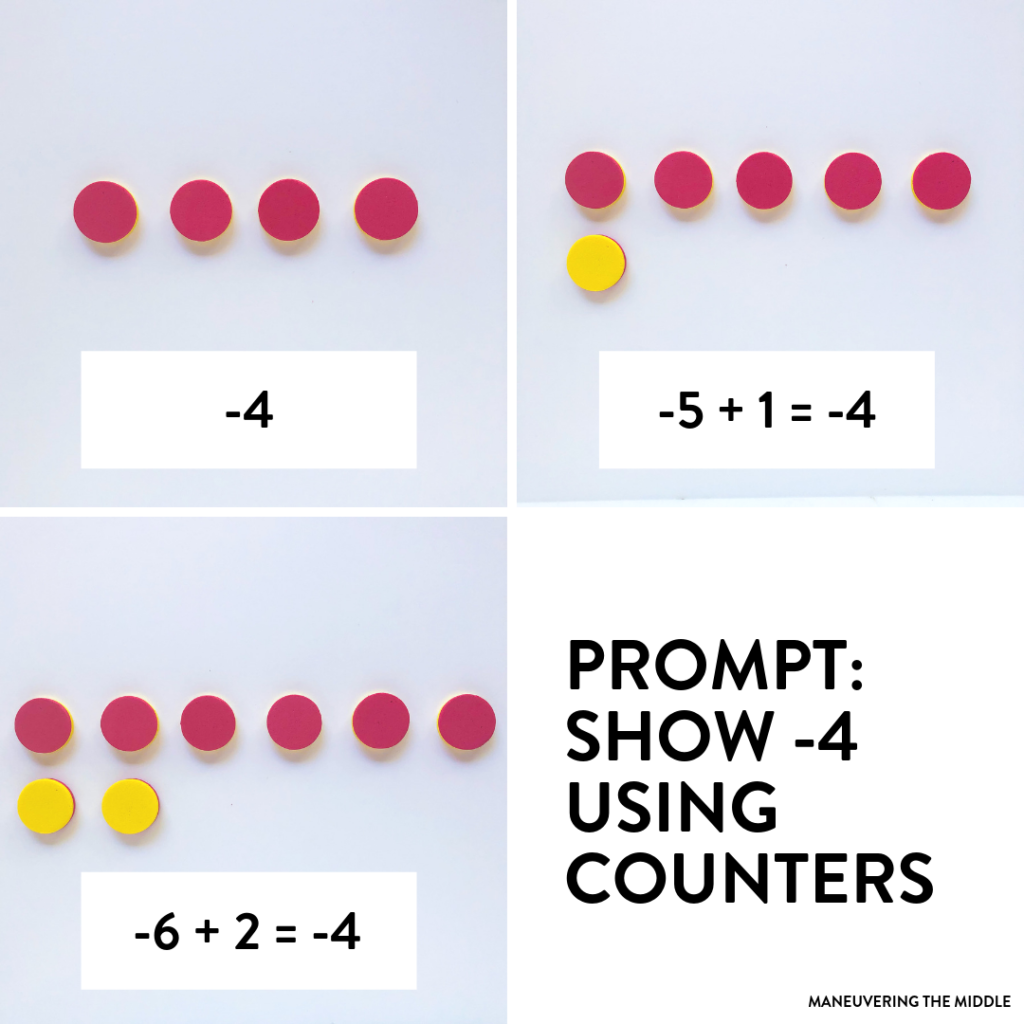
However, they could grab five red counters and one yellow counter, which is still a -4. Once students get the hang of it, you could ask them to work in pairs to produce as many representations as possible within a short time frame. By doing this, you are essentially introducing zero pairs without introducing zero pairs.
Possible prompts:
- How can we make positive 4 with eight counters?
- How many different ways can you show -6?
This helps build integer fluency. It also allows students to be more flexible in their thinking.
Moving Toward the Algorithm
Once students are feeling more confident with models, here is another hands-on way for students to dive deeper into integers. Give students a value they are trying to reach. Provide sticky notes or cards marked with a variety of integers. Students match integers to equal the given value. Similar to using counters, this allows for students to practice their fluency but also to be flexible problem solvers.
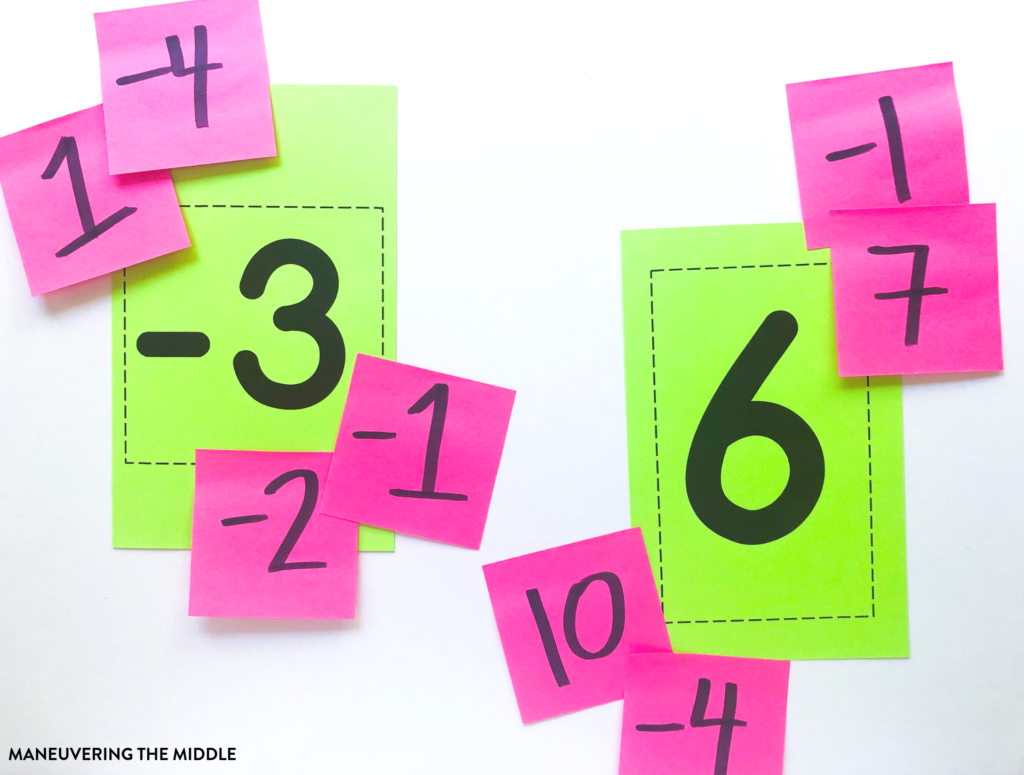
What best practices do you have for teaching integers? Don’t forget to grab your printable vertical number lines here.









Great ideas! Thanks for sharing the hot air balloon example, I’ve never heard that but think it will help to make sense of integer subtraction.
Hi, Brianna – I’m so happy to help!
I love how you incorporated why students are struggling with the concept of integers and how you listed multiple ways we can support students’ conceptual understanding of integers. You mentioned that before teachers jump right into integer operations, they should provide real-world examples of integers. I absolutely agree! It is important to connect classrooms to the real world. Incorporating real world connections into a lesson helps students understand the purpose for what they are learning and how the concepts they learn are useful beyond school.