Is there anything more satisfying than solving a system of equations problem? That might be the nerdiest sentence ever published on this blog, but it is true! I loved learning systems of equations as a student, and I loved teaching it as a teacher. Let’s jump into the 3 methods for mastering systems of equations.
This post is full, so be on the lookout for part 2 where we will discuss various systems activities for your classroom.
Vertical Alignment
Solving systems of equations starts in 8th grade and carries on being explicitly taught in Algebra 2. If you are an 8th grade teacher, you aren’t exactly starting from scratch.
Students will need to be proficient at:
- Solving for a single variable (in this case y) and graphing lines in slope-intercept form (for solving by graphing)
- Rational number operations (for elimination and substitution)
- Combining like terms and distributing (for substitution)
If your students aren’t up to speed with these skills, don’t fret! There is plenty of time to refresh and practice as you introduce systems of equations. I mention this to remind you that students will not be able to solve systems of equations problems without this foundation, so give your students time + practice!

System of Equations Overview
We can often jump in with the methods to solve so quickly that we don’t properly explain what we are solving for apart from saying x and y.
Remind students daily (or even before every problem) that solving systems means we are looking for a solution that makes both equations true! Then reinforce that this is where the lines will intersect on a graph.
Let’s dive into each method for solving systems of equations.
Graphing
The method that I recommend starting with is solving systems of equations by graphing. Due to its visual nature, I find that it makes the abstract nature of solving 2 equations more concrete.
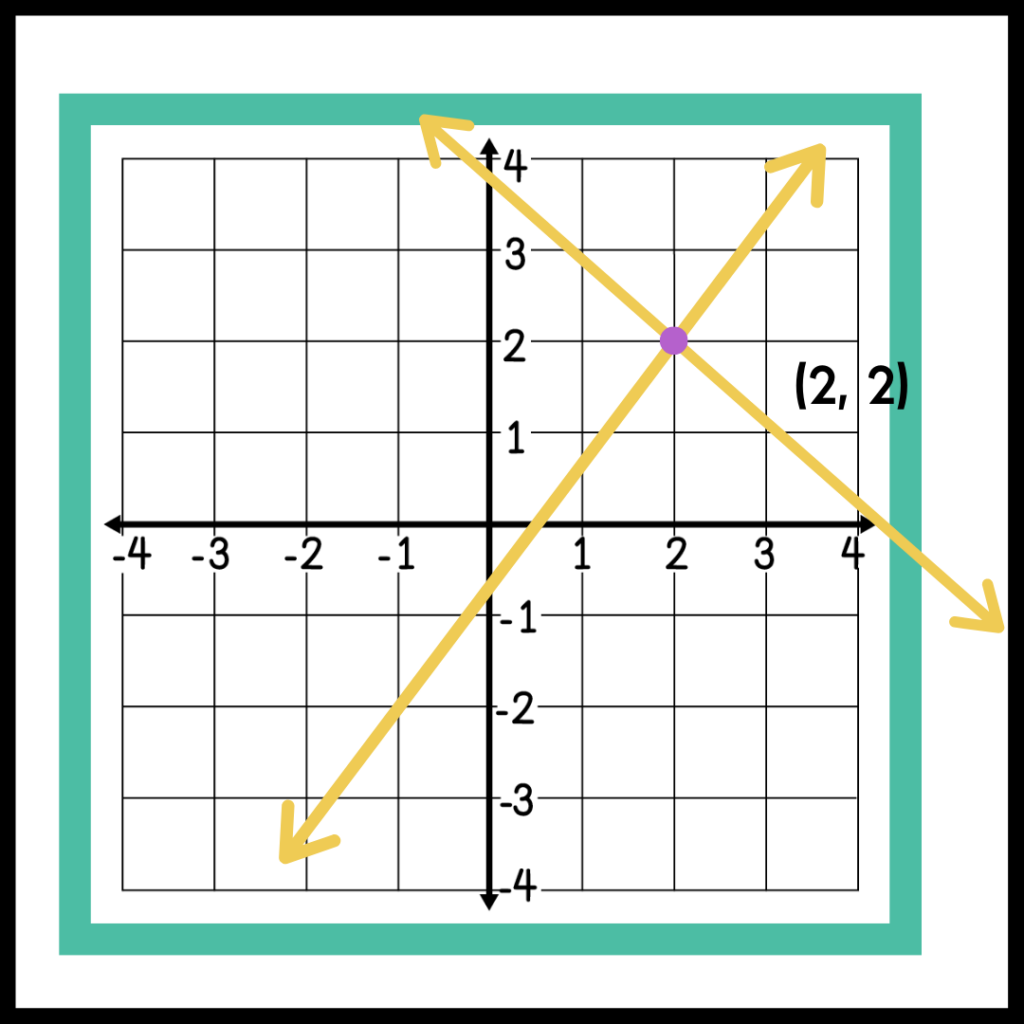
As you introduce this skill, start with the basics of a single line. Remind and reinforce that any point that exists on that single line is a solution to that equation! You can ask students to choose a point on the line, plug in the x and y values, and show them that the equation is a true statement! You can also do the opposite – have students choose and plug in a point that is not on the line to prove that it is not a solution to the equation.
Then you can move to the conclusion that the intersection of two lines is a solution to the system of equations! When students find the point of intersection, plug that point into both equations to find that it is a solution for both equations! (Wow! I am getting pretty excited writing about this!)
Other tips:
- If there was ever time to have your 8th grade or Algebra 1 students move their bodies around, it is this! Arms crossing for one solution, arms parallel for no solution, and arms overlapping for infinitely many solutions.
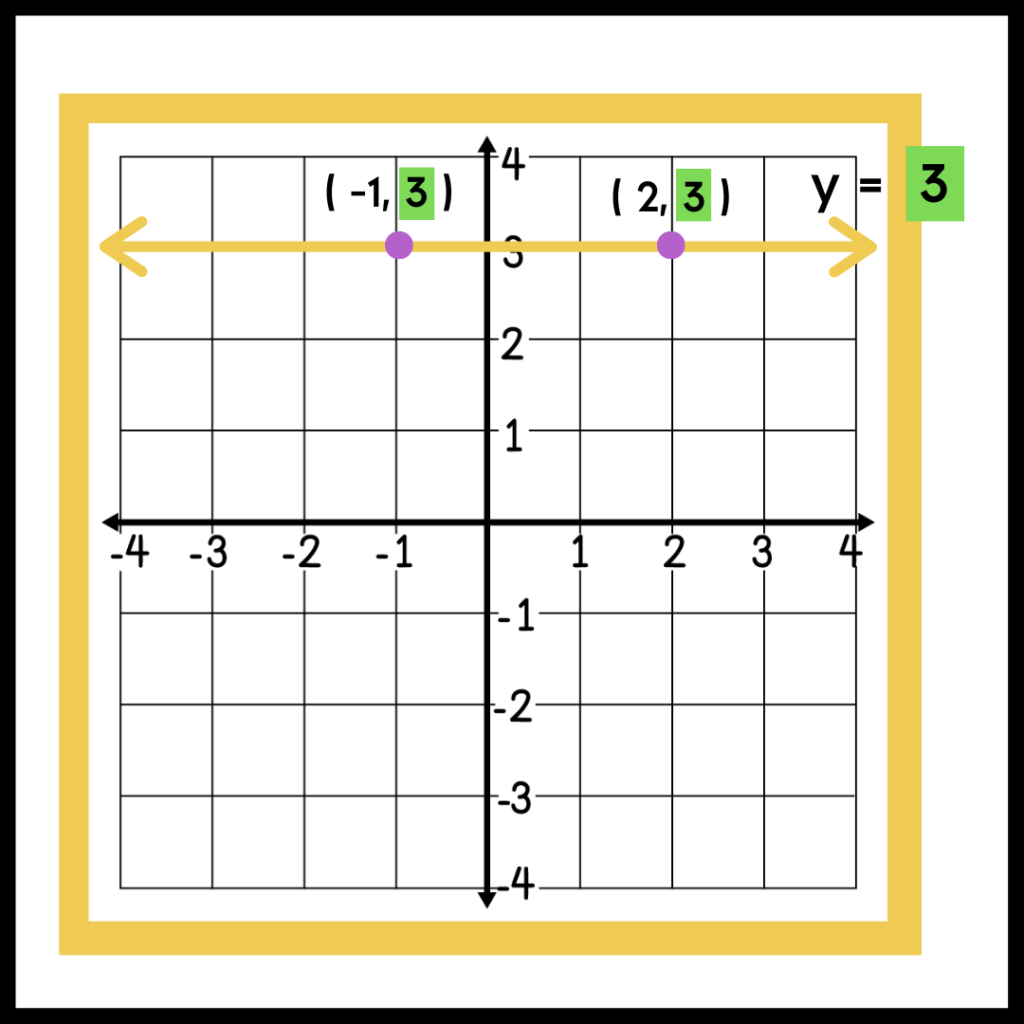
- Students often get stuck with how to graph vertical and horizontal lines, such as y = 3 or x = 2. It is helpful to say it as a sentence, “The y-values will always be equal to 5.” Students can plot 2-3 points with a y-value of 3 and visually see that it will be a horizontal line that also intersects the y-axis at 3.
- Students will have to be proficient at solving for y! In fact, I wrote an entire blog post for this specific skill here.
Substitution
It is my recommendation that substitution is going to require a minimum of 2 days. For it to be done well, I recommend building a strong conceptual foundation of what substitution is before trying to actually solve anything by substituting.
I love these two ideas that I found while researching this topic. This first idea I can attribute to a teacher’s explanation in a Facebook Thread (I am going to summarize with bullet points to make it easier to follow):
- Write a whole number on the board.
- Ask students to write down as many different equivalent expressions of that number
- If the number is 6, then: 3(2), 4+2, 7-1 and so on.
- Make the point that expressions can look different but still be equivalent.
- Next, add variables. x=6, then: x=3+3 and x=3(2).
- Now have students substitute their expressions for x: 3+3 = 3(2).
This blog post breaks down in painstaking detail how a visual aid (stars) makes substitution more concrete. While I used a similar technique with colored Post-it Notes, I think you will benefit from reading this teacher’s methodology.
Other Tips:
- One solution, no solution, infinitely many solutions will still pop up in substitution, so be sure to review. If variables cancel out and the remaining statement is true, the system has infinitely many solutions. Example: 2=2. If variables cancel out and the remaining statement is false, the system has no solution. Example: 2=/=3.
- Distributing and managing negative signs is going to be a common error. Demonstrate and remind students that they can check their work by just plugging solutions in! This goes for elimination too!
- If you need a fun, no-prep, and free activity for substitution, I recommend playing this “Who Wants to Be a Millionaire” style game as a class.
Elimination
This is my personal favorite – maybe it is because I like when standard form actually comes in handy! I am hesitant to admit that I did not know why the elimination method worked until I wrote this post, so I want to share what I learned.
The Additional Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality.
For any expressions, a, b, c, and d,
If a = b
And c = d
Then a+c = b+d
Whenever I present that type of information to my students, I prefer to give a few examples with numbers.
So let’s says a = 2, b = 2, c = 1, and d = 1
If 2=2
And 1=1
Then 2+1 = 2+1
If you didn’t follow that, perhaps this color coded image will make more sense?
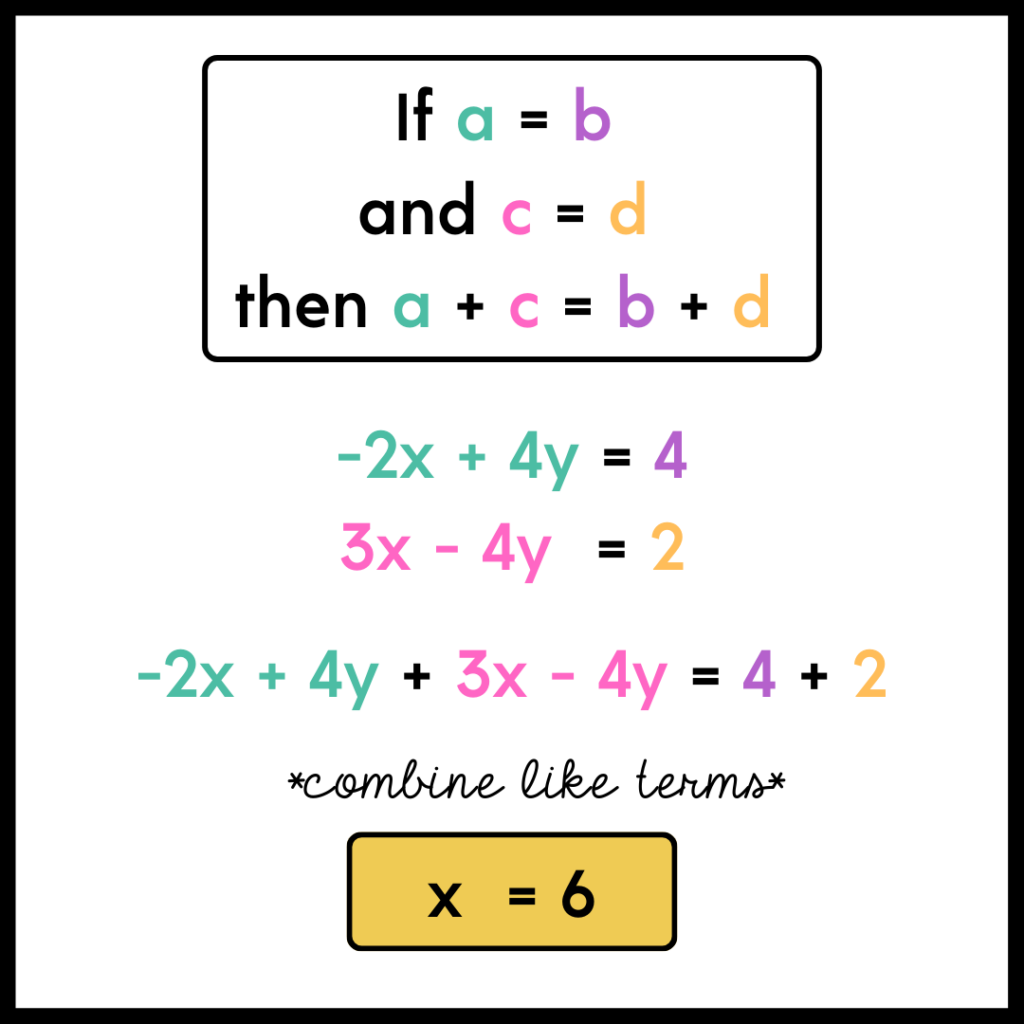
Other Tips:
- Students seem to prefer elimination to substitution! I would give students the opportunity to practice changing y = mx+b into standard form.
- Provide lots of practice multiplying to clear the fractions.
- Don’t forget to go back and solve for the other variable. This is why you should save elimination for after substitution.
What tips would you add to solving the system of equations?





