I will never forget my first day learning long division in third grade – the multiple steps, the division, followed by multiplication…then subtraction?? What?
Fortunately, while that is the only way I ever learned division, there are now numerous other options for division, so students can feel successful. And though I believe the standard division algorithm is a necessity for math, it doesn’t have to be the only way students learn and internalize division.
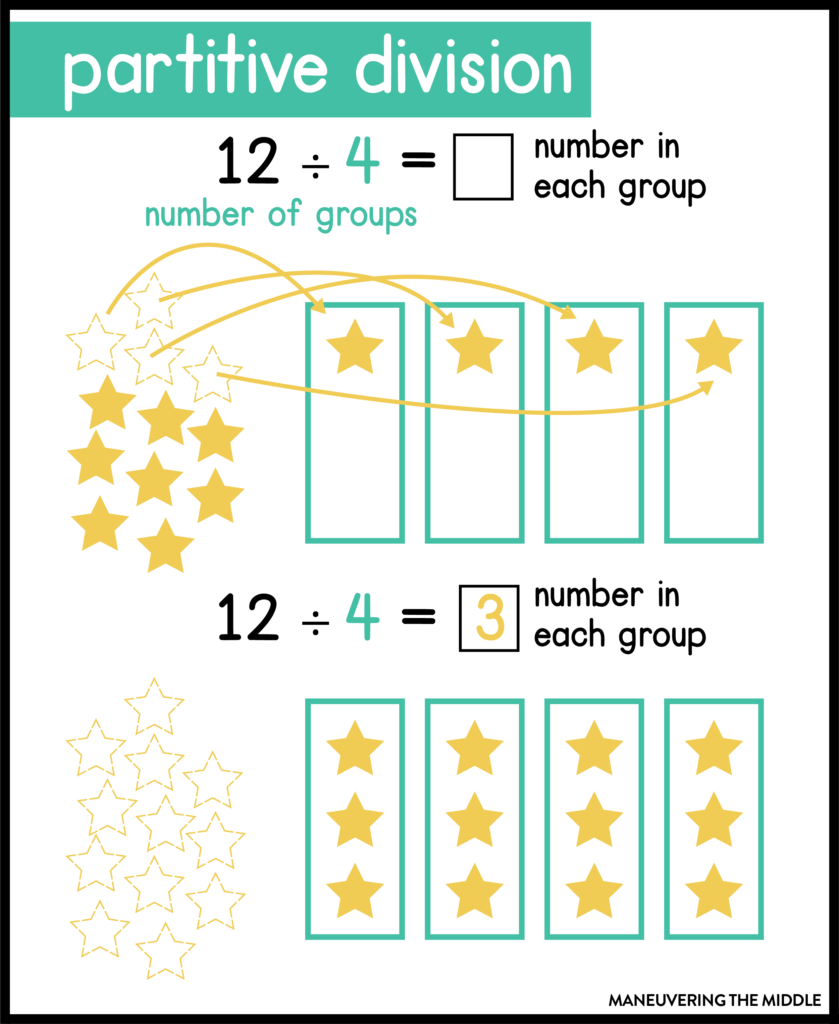
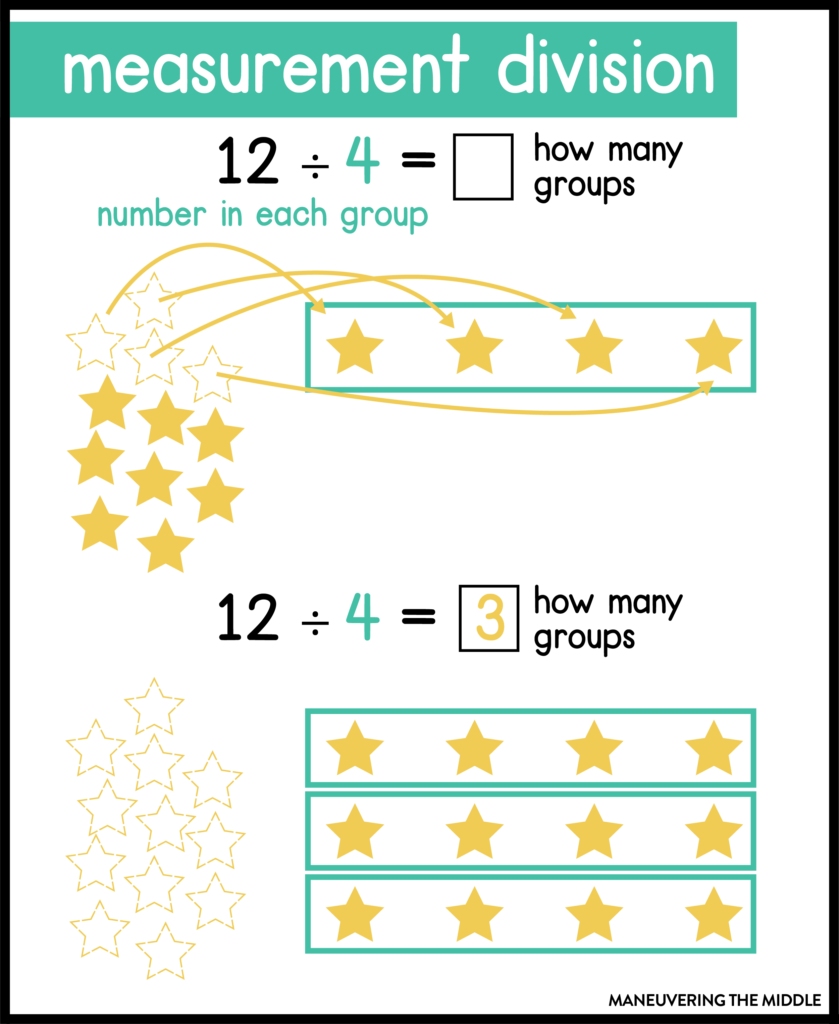
Before we jump into division, a quick reminder of the types of division we have. We have partitive division and measurement division.
In a Partitive division problem, the number of groups is known, and you are solving for the number in each group. Think of it like this – I have 12 cookies and want to divide them evenly by 4 children. How many cookies does each child receive?
In a measurement division problem, the number in each group is known, and you are solving for the number of groups. For example, I have 12 cookies and want to give each child 4 cookies. How many children can receive 4 cookies?
Now that we’ve reviewed the two types of division, here are 4 division strategies to try!
1. Partial Quotient Division
Partial quotient division does exactly what it sounds like – you work to find parts of the quotient (answer) and then add them together to find the overall quotient.
Let’s take 432/18…
Here is a takeaway that will make teaching partial quotient division more accessible for your students; don’t try to have students do all of their multiples of 18 (which is normal when teaching the standard algorithm). It isn’t necessary. Instead, have students do friendly numbers. Depending on your dividend and divisor, this could be 10 or 100. In our case, 10 makes more sense, so 18×10=180. Also, if I go ahead and find 18×2=36, it is painless to find 18×20=360.

Another math tidbit I love is that instead of trying to multiply by 4, it is easier (to me) to multiply by 2 twice.
You can see in the example above, that I was able to find that 18 went into 432 twenty times and then 18 went into 72 four times. I simply add the partial quotients of 20 and 4 to find the quotient of 24.
Lastly, partial quotients are a great tool because students can find the answer in a variety of ways. Take a look below for another way to solve 432/18.

2. Equivalent Ratios
This is a great strategy for division that reinforces ratios! This may not work for every division problem, but it is similar to partial quotients in that you can work in baby steps to get your quotient. Familiarize your students with these division rules:
- Numbers that end in an even number are divisible by 2.
- Numbers that end in a 0 and 5 are divisible by 5.
- Numbers that end in a 0 are divisible by 10.
Once your students have mastered those rules, you can introduce:
- Numbers with the last 2 digits divisible by 4 are divisible by 4 (ex: 1016, 3412, 1004)
- If the sum of the digits is divisible by 3, then the number is divisible by 3 (ex: 342. 3+4+2 = 9. 9 is divisible by 3, therefore, 342 is divisible by 3.)
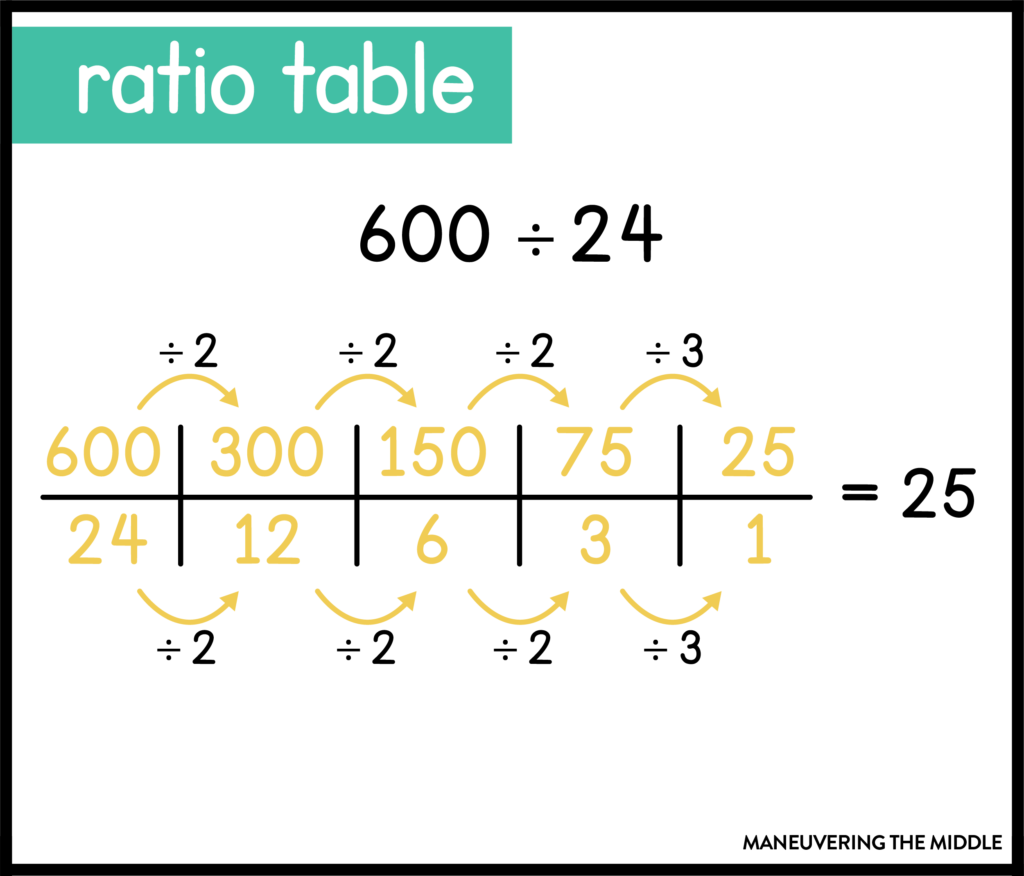
Even if your student cannot get all the way down to 1, they can still divide smaller and more manageable numbers by simplifying. In this example, you can think of it as partitive division, 25 represents the number in 1 group.
3. Multiplying Up
To use the method of Multiplying Up, rewrite the division problem as a multiplication problem. Let’s take the example of 1665/15 =111. Multiplying up asks “15 x ___ = 1655?”
We know that 15×100 = 1500 gets us close to 1665. We can work from there by adding 150 (10 groups of 15) and then again 15 (1 group of 15). 100 + 10 + 1 = 111. Therefore, 1500 + 150 +15 = 1665.

4. Repeated Subtraction
Repeated subtraction is similar to multiplying up (and partial quotient) but backwards. Obviously, these are all related! I think it works best when you are working with dividing numbers with unfriendly divisors (think 3 digit).

Which division strategy will you try with your 5th grade or upper elementary students?
Related content: Check out this post on Dividing Fractions.





