I always loved teaching ratios. Students often did well with the concept, I was able to incorporate fun activities, and we quickly moved on to proportions. With the changes in the Common Core Standards, students are expected to have a much deeper understanding of ratios.
6.RP.1 Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. For example, “The ratio of wings to beaks in the bird house at the zoo was 2:1, because for every 2 wings there was 1 beak.” “For every vote candidate A received, candidate C received nearly three votes.”
6.RP.3 Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
This can be tricky for us as teachers, as it is more complex than what we learned or have experience teaching. I think we are all familiar with 6.RP.1, using ratio language. We often practice writing it three different ways and comparing part-to-part relationships vs. part-to-whole relationships.
When I review the standards, there are a few things that really pop out, specifically 6.RP.3, “use ratio reasoning to solve…”, and the various models noted. I am guilty of often making the leap from ratios to proportions very quickly, while possibly leaving some gaps as to how they are related. I think this is where the specific models come into play.
Ratio Models
The standards specifically mention three models before moving on to equations. I am going to give it my best effort in explaining how they work and what things to make note of when teaching them. As a side note, I would encourage you to use the different models throughout the unit while working problems. It is easy to get in the habit of teaching all three and then only use one for the remainder of the unit. I noticed this during my first year of teaching Algebra in our polynomials unit. I preferred to double distribute; the teacher across the hall preferred the box method. During our common tutorial time, any student in my class double distributed, while all of hers used the box method. It really goes to show that exposing students to the various models regularly helps them be more well-rounded and in the case of these standards, use all three models fluidly.
Tables of Equivalent Ratios
I love this model, mostly because it is so applicable for future math courses, including Algebra. It is easy to draw and takes up less space than the others.
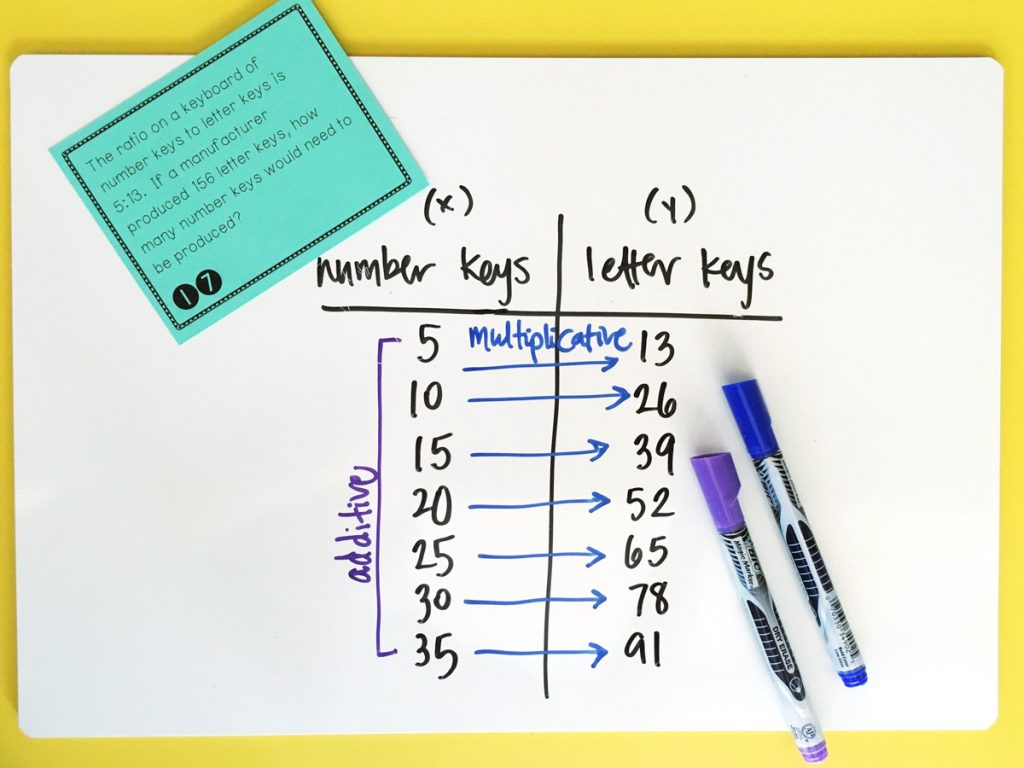
One thing to note about tables with equivalent ratios is that they are both multiplicative and additive. Students frequently miss one of these concepts and then end up with a table that is incorrect. When looking for a missing number in the table, it is essential to understand that because it is a multiplicative relationship, it is “undone” with division. Therefore, you are going to divide y/x. This comes into play in 7th grade with the constant of proportionality and 8th grade with rate of change.
Additionally, there are a few ratio problems that involve changing the ratio. In these cases, it is helpful to add the third column “total” to the ratio table, as well as recognize that there are two different ratios, therefore two tables.
The example above is perfect for a transition to proportions when the time is ready.
Double Number Lines
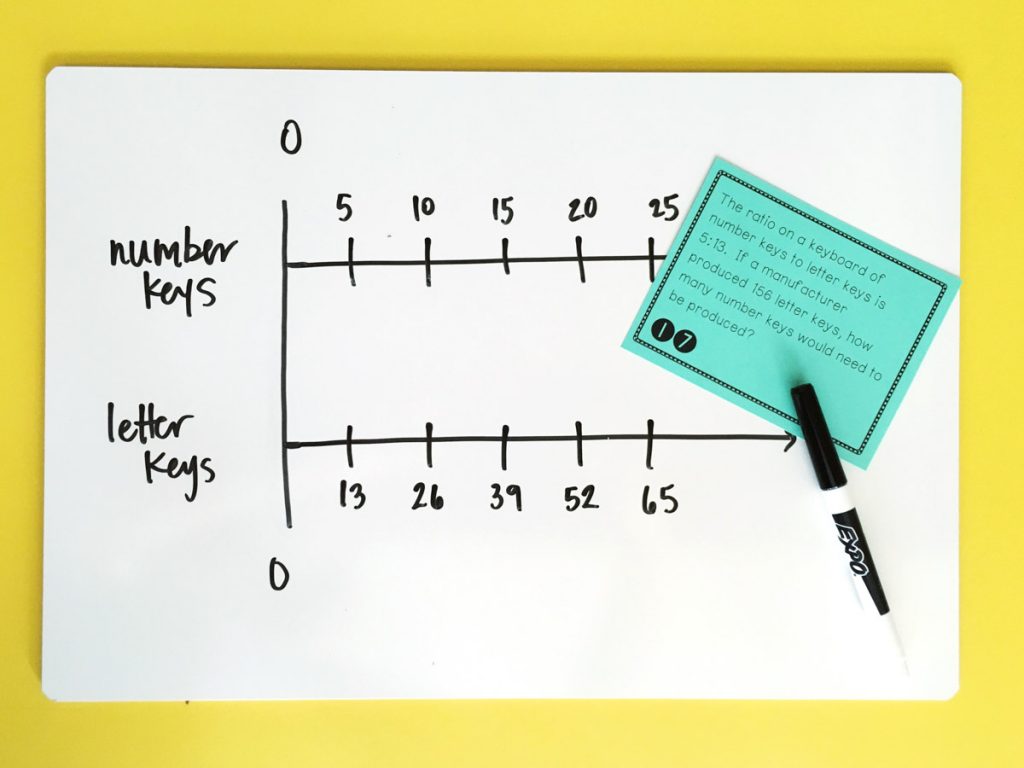I think of the double number line as a horizontal table. It is great for showing students that the relationship is proportional (7th grade). Students might get into trouble here when they don’t have the hashmarks line up correctly and possibly get off track when counting. The benefit to this one is that students are familiar with number lines and that it goes horizontally across the page, thus taking up less space.
Tape Diagrams
Lastly, tape diagrams are a more concrete version of a table or double number line. These might be perfect with students who are struggling to move toward a more abstract understanding and can even be represented with hands-on fraction bars or Cuisinart rods. Be on the lookout for students who draw different sized boxes and thus change the ratio without realizing it.
Common Misconceptions
There are quite a few common misconceptions that students might have. It is helpful to not only address these while teaching but even possibly have students analyze work to see if the misconceptions exist. We often graded famous people’s homework assignments in class to practice error analysis, and it’s perfect for incorporating those mathematical practices. It’s a win-win!
- Mixing up the ratio because they didn’t read the problem
- Not recognizing that the comparison involves the total or difference
- Using addition to describe the relationship
Ideas for Struggling Students
- Sort part-to-part and part-to-whole relationships without working the problems.
- Match situations to the appropriate model.
- Match different models together.
- Practice finding equivalent ratios.
- Given a model, students write a problem.
Ratios provide a foundation to proportional relationships and reasoning. Be sure to spend the necessary time to make sure your students are confident in their reasoning skills and can apply the models appropriately.
Be sure to check out these different concepts and activities that are included in my Ratios Unit and Ratios Activity Bundle.
