When I begin to teach part, whole, and percent problems, I explain to my students that there is nothing that I teach in my class that I use more often in my real life.  Students reflect on where they see percents: the grocery store, sales and discounts, and their grades.

6.RP.A.3.C Find a percent of a quantity as a rate per 100 (e.g., 30% of a quantity means 30/100 times the quantity); solve problems involving finding the whole, given a part and the percent.

6.5(B) Solve real‐world problems to find the whole given a part and the percent, to find the part given the whole and the percent, and to find the percent given the part and the whole, including the use of concrete and pictorial models.

HOW TO TEACH PART, WHOLE, AND PERCENT PROBLEMS

FIRM FOUNDATION OF PROPORTIONS

Before I teach finding part, whole, and percent, students have already practiced and been tested on proportional relationships and unit rates. They are proficient at reading a word problem and setting up a proportion.  What I finally got correct this year is the importance of setting up the labels. I am not talking about writing part/whole; I am referring to describing what the part is in relation to describing the whole.  Example: number of girls/total students.  If students understand that the part is related to the percent by means of the label, then they will be so much more successful in setting up the percent proportion correctly and with more confidence.

SEQUENCE OF TEACHING THE SKILL

Since this is a TEKS readiness skill and a skill with heavy real-world application, I think that it is important to spend several days covering it. Here is an example of how I would sequence the skill over the course of a couple of days.

• Day 1: Percent of a Quantity – Finding the Percent
• Day 2: Percent of a Quantity – Finding the Part
• Day 3: Percent of a Quantity – Finding the Whole
• Day 4: Percent of a Quantity – Mixed

Once students are comfortable solving for each piece in isolation, they need to practice determining which piece they are solving for when the problem type is mixed up. Typically, I give students three problems that are very similar and ask them, “Are we solving for the part, for the whole, or for the percent?” Allow students to grapple with the three different problems and ask them how they know.  This really is key!  If a student can decipher what they are solving for and what the given information is, then it just becomes a multiplication and division problem.  Consider using my prefered problem solving model here.  

1. Mrs. Brack has just set up her Christmas tree.  50 percent of her ornaments are red.  If she has 30 ornaments, then how many are red?

2. Mrs. Brack is setting up her second Christmas tree.  Her tree consists of  30% red and 70% gold ornaments.  If there are 40 red ornaments, then how many ornaments are on the tree?

3. Mrs. Brack is setting up her third Christmas tree.  If there are 25 red ornaments and 35 gold ornaments, then what percent of ornaments are red?

IDEAS FOR STRUGGLING STUDENTS

I teach students to think of “out of 100” when they see the word percent in the word problem. Students are used to having at least three numbers and solving for an unknown fourth when solving proportion word problems.  This can be a bit of a slippery slope as they get older and the problems get more complex, or if there is a table involved.   

In addition, when they see 60%, they are to immediately write it as a fraction – 60 over 100.

Strip diagrams (or percent bars) play a pivotal role in demonstrating the relationship of the percent to the part and whole.  This conceptual understanding helps your visual learners especially and will also show students how you can use benchmark percents (25%, 50%, and 75%) to estimate the answer. 

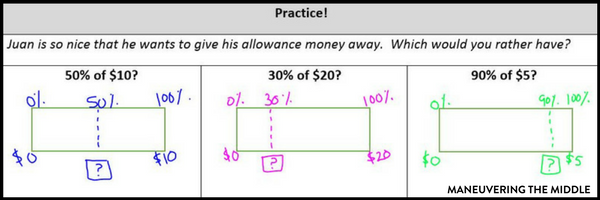
Lastly, use the friendliest numbers you can when introducing the skill!

ANCHOR CHARTS IDEAS

The percent proportion is a helpful tool for students to reference.  I point to it often and I leave it up throughout the year since it is a skill I heavily spiral. In addition, an anchor chart that lists all of the factor pairs of 100 can really help students who struggle solving the proportion using a scale factor.

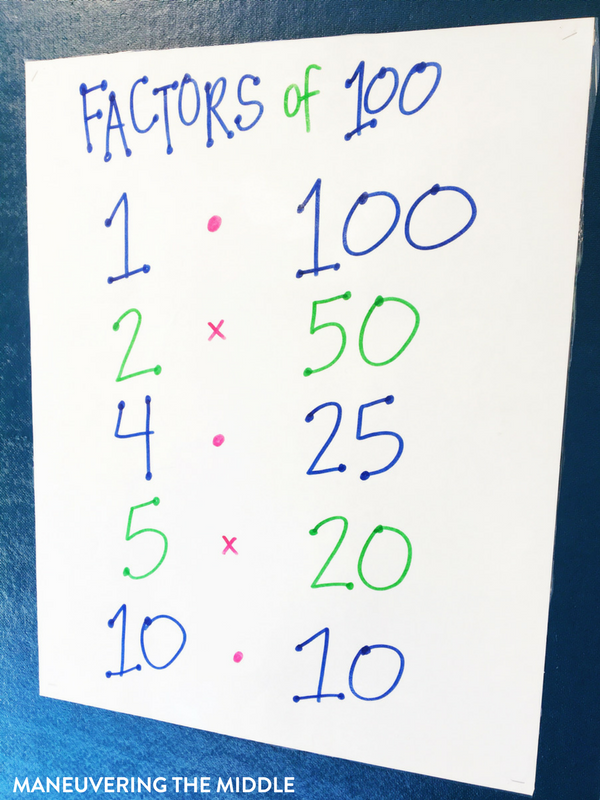
COMMON MISCONCEPTIONS

• Students placing a percent number over another number besides 100
• Unclear if solving for part or whole
• Not fully answering the question; students find the percent but then do not go back and ensure that is what the question is asking for
• Working with percents that are greater than 100 can sometimes throw students for a loop

Do you need resources for teaching percentages to your middle school students? Try All Access!

You can see tips on how to teach inequalities, proportional reasoning, ratios, and fractions/decimals/percents.  What are some ways you teach part, whole, percent?  What other middle school math concepts would you like for us to write about?